K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 6 2023
32D là đúng rồi á bạn
Các phương trình còn lại đều ra R=0 hoặc là vế trái luôn lớn hơn 0 luôn
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
32.
d có 1 vtpt là \(\left(2;-3\right)\) nên cũng nhận các vecto có dạng \(k\left(2;-3\right)\) là vecto pháp tuyến (k khác 0)
Thay \(k=-2\) ta được \(\left(-4;6\right)\) nên C đúng
33. Câu này chỉ có điểm A, ko có điểm M, chắc đề bài ghi sai
Đường thẳng vuông góc d nên nhận (1;-1) là 1 vtpt
Phương trình:
\(1\left(x-1\right)-1\left(y-0\right)=0\Leftrightarrow x-y-1=0\)
34.
Câu này cũng sai luôn, chỉ có C, D chứ ko có 2 điểm AB nào hết????"
\(\overrightarrow{CD}=\left(-1;5\right)\) nên đường thẳng nhận (-1;5) là 1 vtcp
Phương trình: \(\left\{{}\begin{matrix}x=-t\\y=3+5t\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Câu 30:
Để pt đã cho có nghiệm thì:
$\Delta=(2m+5)^2-4(m+\frac{25}{4})\geq 0$
$\Leftrightarrow 4m^2+16m\geq 0$
$\Leftrightarrow m(m+4)\geq 0$
$\Leftrightarrow m\geq 0$ hoặc $m\leq -4$
Đáp án A.
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Câu 31:
Đường trong $(C)$ có tâm $A(1,-5)$ và bán kính $R=\sqrt{45}$
Vì ĐT cần tìm song song với $x+2y+5=0$ nên nó có dạng $(I):x+2y+m=0$
$(I)$ là tiếp tuyến của $(C)$ nên:
\(d(A,(I))=R\Leftrightarrow \frac{|1-2.5+m|}{\sqrt{1^2+2^2}}=\sqrt{45}\)
$\Rightarrow m=24$ hoặc $m=-6$
Đáp án C.
8 tháng 5 2021
Câu 30 :
- Gọi PT tiếp tuyến là denta .
- Ta có denta vuông góc với d
=> PTTQ denta có dạng : \(3x+2y+c=0\)
- Xét đường tròn ( C ) có : \(\left\{{}\begin{matrix}I\left(-2;1\right)\\R=\sqrt{13}\end{matrix}\right.\)
Mà PT denta là tiếp tuyến của (C)
\(\Rightarrow R=d_{\left(denta/I\right)}=\sqrt{13}=\dfrac{\left|3.\left(-2\right)+2.1+c\right|}{\sqrt{13}}\)
\(\Rightarrow\left|c-4\right|=13\)
\(\Rightarrow\left[{}\begin{matrix}c-4=13\\c-4=-13\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=17\\c=-9\end{matrix}\right.\)
Vậy .... Đáp án C .
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2021
32.
\(sin^4x=\left(sin^2x\right)^2=\left(\dfrac{1-cos2x}{2}\right)^2=\dfrac{1}{4}-\dfrac{1}{2}cos2x+\dfrac{1}{4}cos^22x\)
\(\)\(=\dfrac{1}{4}-\dfrac{1}{2}cos2x+\dfrac{1}{4}\left(\dfrac{1}{2}+\dfrac{1}{2}cos4x\right)\)
\(=\dfrac{3}{8}-\dfrac{1}{2}cos2x+\dfrac{1}{8}cos4x\)
\(a+b+2c=\dfrac{3}{8}-\dfrac{1}{2}+2.\left(\dfrac{1}{8}\right)=\dfrac{1}{8}\)
33.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta=m^2-4m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< 4\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3\right\}\) có 3 giá trị
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
ABC vuông cân \(\Rightarrow\left\{{}\begin{matrix}AC=AB=3\\BC=AB\sqrt{2}=3\sqrt{2}\end{matrix}\right.\)
\(\overrightarrow{BC}.\overrightarrow{CA}=-\overrightarrow{CB}.\overrightarrow{CA}=-BC.AC.cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\sqrt{2}.3.cos45^0=-9\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)
28 tháng 8 2016
1312 : ( 3x - 19 ) = 32
\(\Rightarrow3x-19=1312:32\)
\(\Rightarrow3x-19=41\)
\(\Rightarrow3x=41+19\)
\(\Rightarrow3x=60\)
\(\Rightarrow x=60:3\)
\(\Rightarrow x=20\)
Vậy x=20
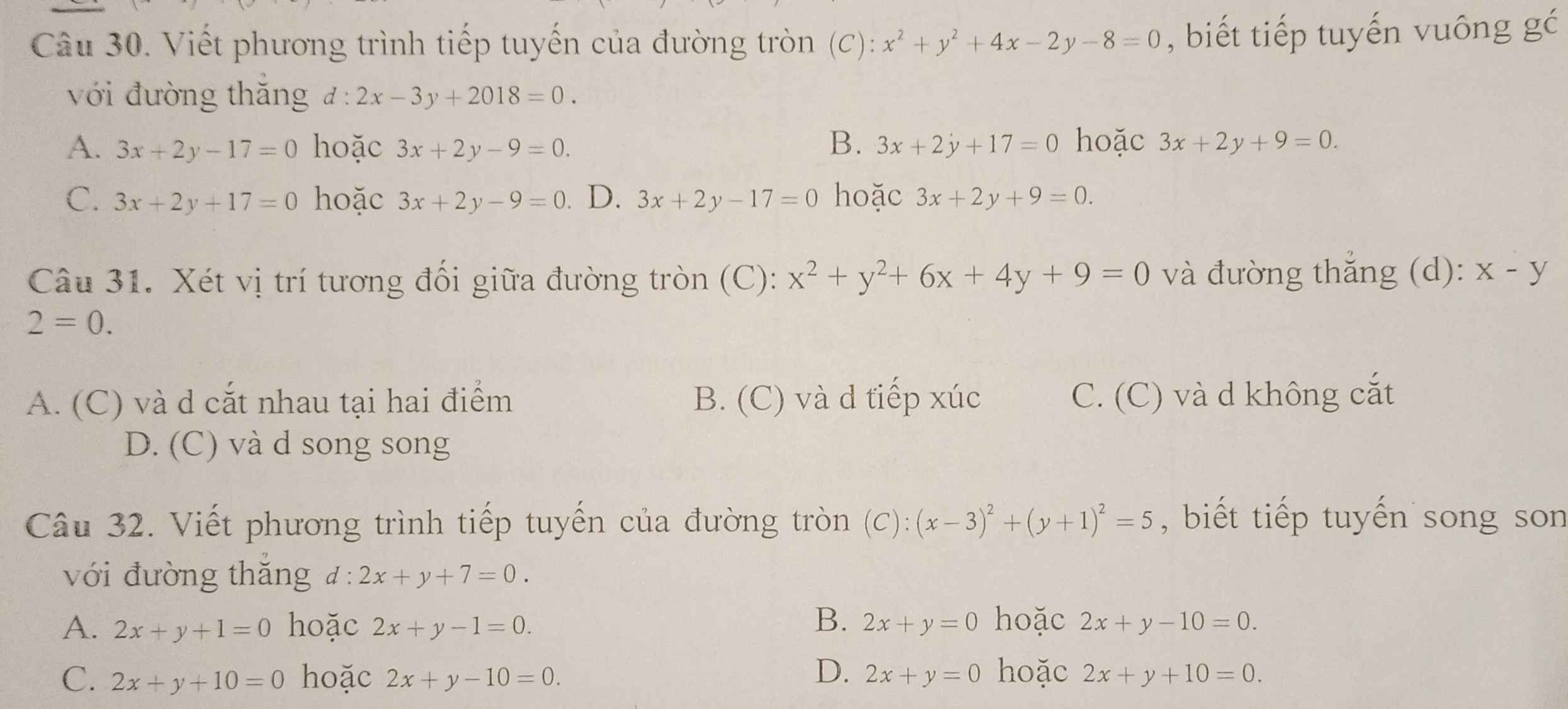
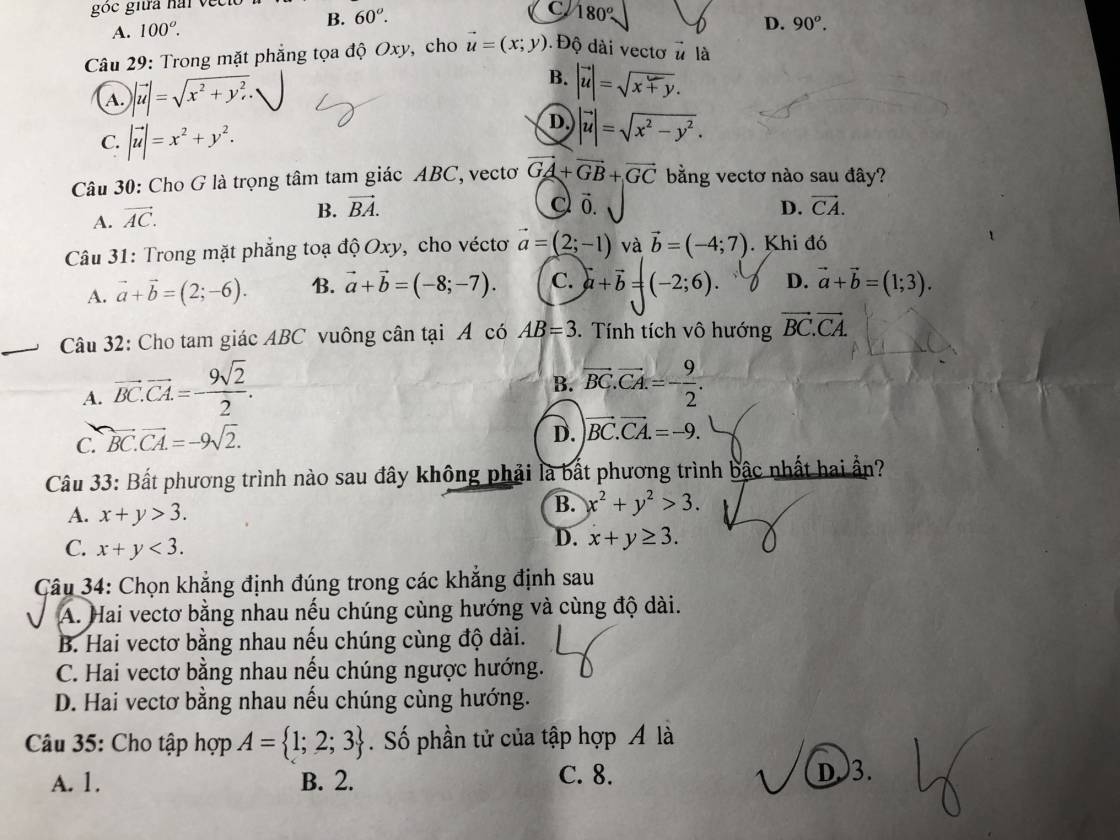
Không có đáp án nào đúng cả bạn ạ.