Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sai số ngẫu nhiên được xác định như sau:
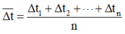
Trong đó:
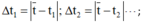
Sai số dụng cụ Δt’ thông thường có thể lấy bằng nửa hoặc một độ chia nhỏ nhất. Ở đây, qua giá trị trong bảng ta thấy phép đo thời gian có sai số dụng cụ với độ chia nhỏ nhất là 0,001s → Δt’ = 0,001s
Tính toán ta thu được bảng số liệu sau:
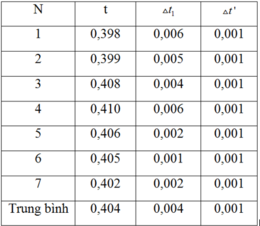


Để tính kết quả của phép đo thời gian rơi tự do của vật, ta cần lấy trung bình của các kết quả đo và trừ đi sai số của đồng hồ đo.
Trung bình của các kết quả đo là: (0,404 + 0,406 + 0,403) / 3 = 0,4043 s.
Sai số của đồng hồ đo là 0,001 s.
Vậy, kết quả của phép đo thời gian rơi tự do của vật được ghi là 0,4043 - 0,001 = 0,4033 s.

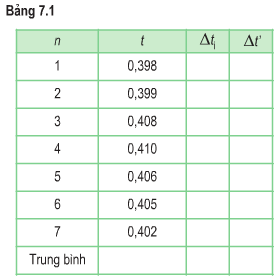
|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |


Các em thực hành theo hướng dẫn của giáo viên.
Ví dụ cho kết quả thí nghiệm
Bảng 6.1
Quãng đường: s = 0,5 (m)

- Tốc độ trung bình: \(\overline v = \frac{s}{{\overline t }} = \frac{{0,5}}{{0,778}} = 0,643(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0,002 + 0,002}}{3} \approx 0,002(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,002}}{{0,778}}.100\% = 0,3\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,0005}}{{0,5}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 0,3\% = 0,4\% \\\Delta v = \delta v.\overline v = 0,4\% .0,643 = 0,003\\ \Rightarrow v = 0,643 \pm 0,003(m/s)\end{array}\)
Bảng 6.2
Đường kính của viên bi: d = 0,02 (m); sai số: 0,02 mm = 0,00002 (m)

- Tốc độ tức thời: \(\overline v = \frac{d}{{\overline t }} = \frac{{0,02}}{{0,032}} = 0,625(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0 + 0,00}}{3} \approx 0,001(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,001}}{{0,032}}.100\% = 2,1\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,00002}}{{0,02}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 2,1\% = 2,2\% \\\Delta v = \delta v.\overline v = 2,2\% .0,0032 = 0,001\\ \Rightarrow v = 0,625 \pm 0,014(m/s)\end{array}\)
Nhận xét: Tốc độ trung bình gần bằng tốc độ tức thời, vì viên bi gần như chuyển động đều.

L = a t 2 2 ⇒ a ¯ = 2 L t 2 = 2 . 2 4 , 2 2 = 0 , 23 m / s 2
L = a t 2 2 ⇒ a = 2 L t 2 ⇒ ∆ a a = ∆ L L + 2 ∆ t t = 0 , 005 2 + 2 0 , 2 4 , 2 = 0 , 0977
⇒ ∆ a = 0 , 09 π . a ¯ = 0 , 022 m / s 2
Vậy a = (0,23 ± 0,02) ( m / s 2 )


\(\overline{v}=\dfrac{s}{t}=\dfrac{0,5}{0,778}=\dfrac{250}{389}\approx0,643m/s\)
\(\overline{\Delta t}=\dfrac{\Delta t_1+\Delta t_2+\Delta t_3}{3}=\dfrac{\left|0,778-0,777\right|+\left|0,778-0,780\right|+\left|0,778-0,776\right|}{3}=\dfrac{1}{600}\)
\(\delta t=\dfrac{\overline{\Delta t}}{t}\cdot100\%;\delta s=\dfrac{\overline{\Delta s}}{s}\cdot100\%\)
\(\delta v=\delta s+\delta t=0,1\%\)
\(\Delta v=\delta v\cdot\overline{v}=0,1\%\cdot\dfrac{250}{389}\approx0,00064\)
Phép đo tốc độ trung bình là \(v=0,643\pm0,00064\)
bảng kia là làm word nha