Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc lò xo dao động điều hoà theo phương thẳng đứng
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn: ∆l.
Ta có:
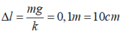
Từ vị trí cân bằng dời vật đoạn 12cm theo phương lò xo rồi buông cho dao động điều hòa => A = 12cm Vì A > ∆l nên lực đàn hồi cực tiểu tác dụng lên vật bằng 0

Chọn D
+ A = 5 (cm)
![]()
![]()
![]()
![]()
![]()
Vậy giá trị cực tiểu và cực đại của lực đàn hồi của lò xo là 1N và 3N.

Đáp án B.
Độ dãn của lò xo tại vị trí cân bằng là
Δ l 0 = m g k = 10 cm
Từ vị trí cân bằng nâng vật lên một đoạn 5 cm rồi buông nhẹ cho vật dao động điều hòa nê n biên độ A = 5 cm
Lực đàn hồi cực tiểu của lò xo tác dụng lên vật trong quá trình dao động bằng F d h min = k ( Δ l 0 − A ) = 1 (N)

Đáp án B
Độ dãn của lò xo tại vị trí cân bằng là D l 0 = m g k = 10 c m
Từ vị trí cân bằng nâng vật lên một đoạn 5cm rồi buông nhẹ cho vật dao động điều hòa nên biên độ A = 5cm
Lực đàn hồi cực tiểu của lò xo tác dụng lên vật trong quá trình dao động bằng Fđhmin k ( D l 0 - A ) = 1 ( N )

Đáp án A
Ta có ∆l = mg/k = 0,025 m = 2,5 cm.
![]()
![]()
![]()
→ quãng thời gian ![]() ngược chiều nhau là T/6 →
ngược chiều nhau là T/6 →
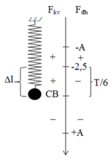 vật
vật
đi từ vị trí π/2 đến 2π/3 và -2π/3 đến –π/2.
→ -A/2 = 2,5 cm.
→ A = 5 cm.

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)


