Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ tại vị trí xe hãm phanh.
Chiều \(\left(+\right)\) là chiều chuyển động \(\left(v\ge0\right)\).
Gốc thời gian là thời điểm xe hãm phanh.
Lúc \(t=0\) thì \(v_0=72km/h=20m/s\)
\(t=10s\) thì \(v=0\)
\(a,a=?m/s^2\)
Ta có : \(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{10}=\dfrac{0-20}{10}=-2m/s^2\)
\(b,s=?m\)
Ta có : \(d=v_0t+\dfrac{1}{2}at^2=20.10+\dfrac{1}{2}\left(-2\right).10^2=100\left(m\right)\)
Do \(v\ge0\Rightarrow s=d=100m\)
\(c,\) Quãng đường đi được của xe trong 8s đầu là :
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=20.8+\dfrac{1}{2}\left(-2\right).8^2=96\left(m\right)\)
Quãng đường đi được của xe trong 2s cuối là : \(s-s_1=100-96=4\left(m\right)\)
Vì quãng đường trong 2s đầu và 2s cuối có cùng thời gian nên ta có s của 2s đầu và cuối bằng nhau.
Vậy ...

Chọn đáp án C
? Lời giải:
+ Xe chuyển động chậm dần đều nên a không đổi.
+ Gọi v0 là vận tốc của xe trước thời điểm dừng lại 1 s
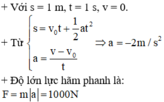


a) Công thức tính vận tốc lúc sau (lúc xe dừng lại):
\(v_1=v_0+at\Rightarrow0=v_0+5a\left(1\right)\)
Công thức tính quãng đường xe đi được từ lúc hãm phanh cho đến khi dừng hẳn:
\(s=v_0t+\dfrac{1}{2}at^2\Rightarrow15=5v_0+\dfrac{25}{2}a\left(2\right)\)
Từ (1), (2) ta có hệ: \(\left\{{}\begin{matrix}v_0+5a=0\\2v_0+5a=6\end{matrix}\right.\)
Giải hệ trên, ta được: \(\left\{{}\begin{matrix}v_0=6\left(\dfrac{m}{s}\right)\\a=-1,2\left(\dfrac{m}{s^2}\right)\end{matrix}\right.\)
Tốc độ trung bình của xe trong khoảng thời gian trên là: \(v_{tb}=\dfrac{s}{t}=\dfrac{15}{5}=3\left(\dfrac{m}{s}\right)\)
b) Chọn hệ quy chiếu là hệ trục toạ độ Oxy như hình vẽ.
Theo định luật II Newton, ta có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_c}=m.\overrightarrow{a}\left(1\right)\)
Chiếu (1) lên trục Ox, ta có:
\(-F_c=m.a\Rightarrow F_c=m.\left(-a\right)=2.\left(-\dfrac{-6}{5}\right)=2,4\left(N\right)\)
Quãng đường xe đi được trong giây thứ tư là:
\(s=s_{4s}-s_{3s}=\left(6.4+\dfrac{1}{2}.\dfrac{-6}{5}.4^2\right)-\left(6.3+\dfrac{1}{2}.\dfrac{-6}{5}.3^2\right)=1,8\left(m\right)\)