Câu 2. [VDT] Với giá trị nào của m thì 2 đường thẳng y = (2+m)x + 1 và y = 2x + m cắt nhau tại một điểm có hoành độ bằn...

hung

8 tháng 1 2022

Câu 2. [VDT] Với giá trị nào của m thì 2 đường thẳng y = (2+m)x + 1 và y = 2x + m cắt nhau tại một điểm có hoành độ bằng –2

A. m = 4. B. m = . C. . D. m = .

Câu 3. [VDT] Xác định giá trị của m để đường thẳng y = (m – 3)x + 2 đi qua giao điểm của 2 đường thẳng: y = 3x +1 và y = – x – 3. Kết quả

A. m=3. B. m = – 3 . C. m = 7 . D. m = 5.

Câu 4. [VDT] Một máy bay bay với vận tốc 170m/s lên cao

theo phương tạo với đường băng một góc 40⁰. Hỏi sau 6 phút,

máy bay ở độ cao bao nhiêu mét so với mặt đất?

(kết quả làm tròn đến hàng đơn vị)

A. 39340 m. B. 39341 m.

C. 39338 m. D. 39339 m.

Câu 5. [TH] Cho đường tròn (O) có bán kính OA = R. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Độ dài dây BC bằng

A. R . B. . C. R . D. .

Câu 6. [VDT] Cho đường tròn (O) có bán kính R = 10cm ngoại tiếp tam giác đều ABC. Độ dài cạnh của tam giác đều bằng

A. 5 cm. B. cm. C. cm. D. 5cm.

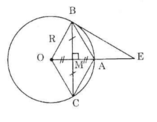
Câu 7. [VDT] Cho đường tròn (O; 6cm) và dây AB = 8 cm. Đường thẳng qua O vuông góc với AB và cắt tiếp tuyến của đường tròn (O) tại A ở điểm C. Độ dài OC bằng

A. 15cm. B. 18 cm. C. 20 cm. D. 22 cm.

Câu 8. [VDT] Cho hai đường tròn (O; 8cm) và (O^/; 5cm) tiếp xúc ngoài tại M. Gọi AB là tiếp tuyến chung của hai đường tròn (A (O); B (O^/)). Tính độ dài AB (kết quả làm tròn đến chữ số thập phân thứ hai).

A. 8.75 cm. B. 10,85 cm. C. 12,65 cm. D. 14,08 cm.

Câu 9. [VDC] Cho hai đường tròn bằng nhau (O; R) và (O^/; R) cắt nhau tại A và B sao cho tâm đường tròn này nằm trên đường tròn kia. Tính theo R diện tích tứ giác OAO^/B

A. . B. . C. . D. .

Câu 10. [VDC] Cho tam giác đều ABC có cạnh bằng 7 cm.

Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và bán kính

đường tròn nội tiếp tam giác ABC (như hình vẽ). Tổng R + r bằng

A. cm. B. cm.

C. cm. D. cm.

Câu 11. [VDC] Cho hai đường tròn (O; 10cm) và (O^/; 6cm) tiếp xúc ngoài tại M. Gọi AB là tiếp tuyến chung của hai đường tròn (A (O); B (O^/)). Đường thẳng AB cắt đường thẳng OO^/ tại C. Độ dài O^/C bằng

A. 16cm. B. 24 cm. C. 28 cm. D. 34 cm.

Câu 12. [VDC] Cho tam giác ABC có đường tròn nội tiếp tiếp xúc với AB, BC, CA theo thứ tự tại M, N, P; Biết BC = a và chu vi tam giác ABC bằng p. Tính AM theo a và p.

A. AM = p + a. B. AM = p -2a.

C. AM = 2p – a. D. AM = – a.

#Toán lớp 9