
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


41.
Số hạng tổng quát của khai triển \(\left(x^2+x\right)^{10}\):
\(T_{k+1}=C^k_{10}.\left(x^2\right)^{10-k}.x^k=C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}\)

a. Năm số hạng đầu của dãy số
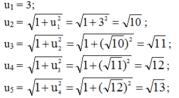
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
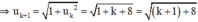
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

Ta có:
\(u_n=u_1+\left(n-1\right)d\\ =4+\left(n-1\right)\cdot\left(-10\right)\\ =4-10n+10\\ =14-10n\)

Để \(u_n\) có tận cùng là 7 thì \(6^n+1\) có tận cùng là 7
=>\(6^n\) có chữ số tận cùng là 6
=>\(n\in Z^+\)
\(69000< U_n< 960000\)
=>\(69000< 6^n+1< 960000\)
=>\(68999< 6^n< 959999\)
=>\(log_668999< n< log_6959999\)
=>\(6,22< n< 7,68\)
mà n là số tự nhiên
nên n=7
=>Có 1 số hạng duy nhất thỏa mãn
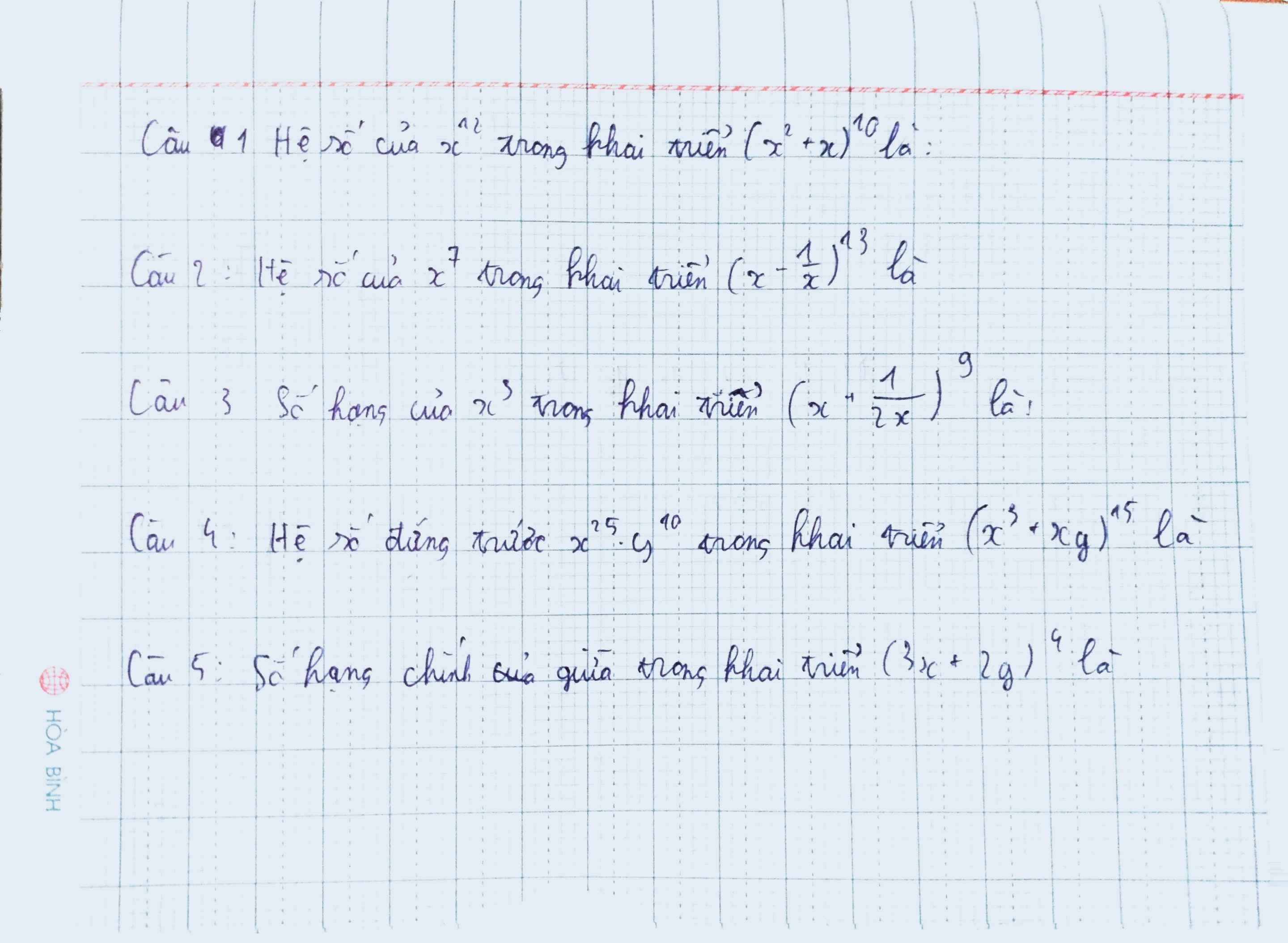

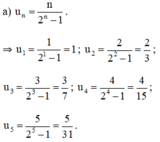
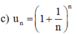
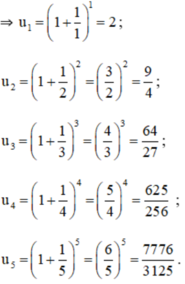
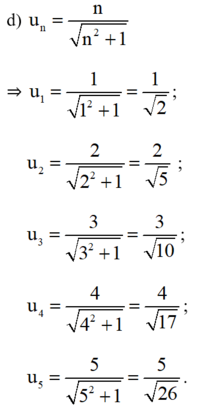
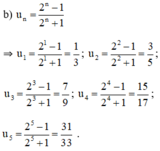
1.
\(\left(x^2+x\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}.\left(x^2\right)^{10-k}.x^k=\sum\limits^{10}_{k=0}C^k_{10}.x^{20-k}\)
\(\Rightarrow20-k=12\Rightarrow k=8\)
\(\Rightarrow\) Hệ số của \(x^{12}\) trong khai triển \(\left(x^2+x\right)^{10}\) là: \(C^8_{10}=45\)
2.
\(\left(x-\dfrac{1}{x}\right)^{13}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-k}.\dfrac{1}{x^k}=\sum\limits^{13}_{k=0}C^k_{13}.x^{13-2k}\)
\(\Rightarrow13-2k=7\Rightarrow k=3\)
\(\Rightarrow\) Hệ số của \(x^7\) trong khai triển \(\left(x-\dfrac{1}{x}\right)^{13}\) là: \(C^3_{13}=286\)