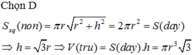Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
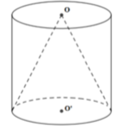
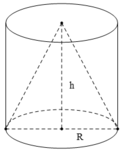
Gọi ABCD.A'B'C'D' là hình lăng trụ nội tiếp hình trụ. Khi đó lăng trụ đã cho là lăng trụ đứng và có chiều cao là chiều cao h của hình trụ. Vậy thể tích khối lăng trụ đạt giá trị lớn nhất khi và chỉ khi diện tích đáy ABCD đạt giá trị lớn nhất. Do ABCD nội tiếp đường tròn đáy của hình trụ nên ta có:
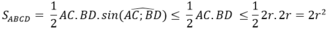
Dấu bằng xảy ra khi ABCD là hình vuông. Vậy thể tích khối lăng trụ tứ giác nội tiếp hình trụ lớn nhất là V = 2 r 2 h

Chọn A.
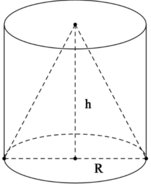
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V1 = πR2 h.
Hình nón có bán kính đáy R và chiều cao h nên thể tích ![]()
Từ đó suy ra V1 = 3V2.

Đáp án C
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V 1 = π R 2 h.
Hình nón có bán kính đáy R và chiều cao h nên thể tích V 2 = 1/3 π R 2 h.
Từ đó suy ra V 1 = 3 V 2 .

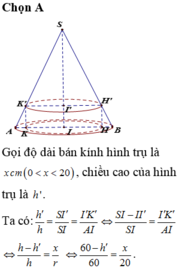
Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25