Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

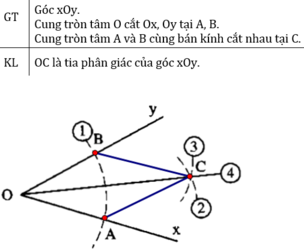
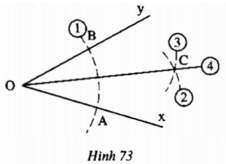
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
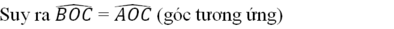
nên OC là tia phân giác của góc xOy.

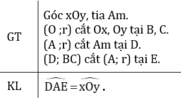
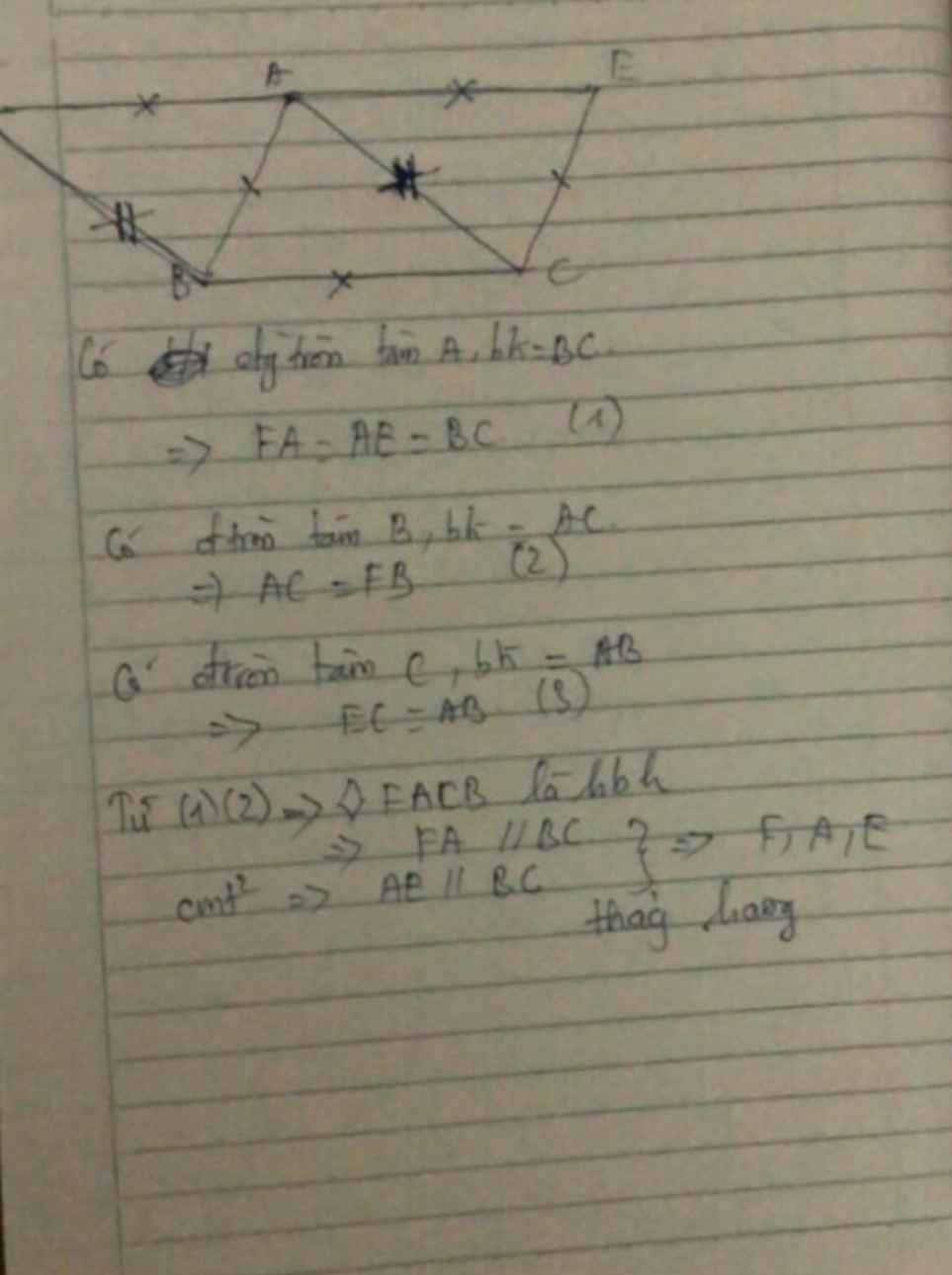
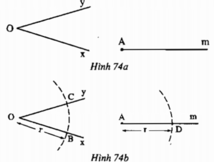
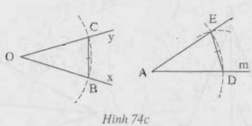
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
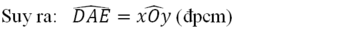

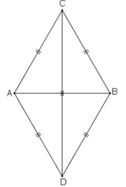
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

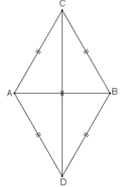
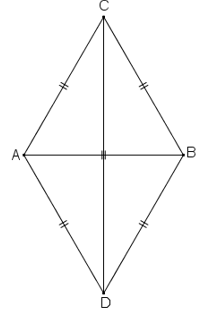
Xét ΔACD và ΔBCD, ta có:
AC = BC (= AB)
CD cạnh chung
AD = BD (= AB)
Suy ra: ΔACD = ΔBCD(c.c.c)
bạn vũ minh tuấn chép nguyên của tech 12h ạ
Tham khảo nhé:
Câu 1:
Câu 2:
Chúc bạn học tốt!