K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
18 tháng 1 2018
Đáp án C
giả sử ![]()
The giả thiết, ta có
![]()
![]()
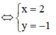
Suy ra ![]()
Ta có ![]()
![]()
Vậy chọn phần ảo là – 1

CM
5 tháng 8 2018
Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
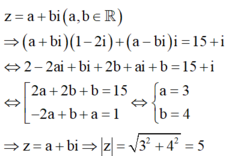
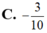
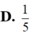


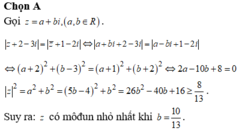
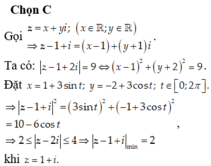


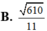

1/Áp dụng công thức tổng cấp số nhân:
\(z=1+\left(1+i\right)+\left(1+i\right)^2+...+\left(1+i\right)^{20}=1+\frac{\left(1+i\right)^{21}-1}{i+1-1}=1+\frac{\left(1+i\right)^{21}-1}{i}\)
Ta có:
\(\left(1+i\right)^{21}=\left(1+i\right)\left[\left(1+i\right)^2\right]^{10}=\left(1+i\right)\left(1+2i+i^2\right)^{10}\)
\(=\left(1+i\right)\left(2i\right)^{10}=\left(1+i\right).2^{10}.i^{10}=\left(1+i\right)2^{10}\left(i^2\right)^5=-\left(1+i\right).2^{10}\)
\(\Rightarrow z=1+\frac{-\left(1+i\right)2^{10}-1}{i}=1+\frac{-i\left(1+i\right)2^{10}-i}{i^2}=1+\left(i+i^2\right)2^{10}+i=1+i+\left(i-1\right).2^{10}\)
\(\Rightarrow z=\left(1-2^{10}\right)+\left(1+2^{10}\right)i\)
2/
\(z=\left(3+i\sqrt{3}\right)^3\Rightarrow\frac{1}{z}=\frac{1}{\left(3+i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(3+i\sqrt{3}\right)^3\left(3-i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(9-3i^2\right)^3}\)
\(\Rightarrow\frac{1}{z}=\frac{\left(3-i\sqrt{3}\right)^3}{12^3}=\left(\frac{1}{4}-\frac{\sqrt{3}}{12}i\right)^3\)
3/ Bạn viết lại đề được không?
Cảm ơn nhiều ạ! Mình làm được rồi ạ!