Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TA có: \(y=-x^4+4x^2-3\)
\(=-\left(x^4-4x^2+4\right)+1\)
\(=-\left(x^2-1\right)^2+1\le1\)
Vì \(y\in\left[-2;3\right]\)
=>..........................
Đến đây dễ rồi bạn tự làm nốt nhé

y = (x² - 1)(x + 3)(x + 5)
= [(x - 1)(x + 5)].[(x + 1)(x + 3)]
= (x² + 4x - 5)(x² + 4x + 3)
= [x² + 4x - 1) - 4].[(x² + 4x - 1) + 4]
= (x² + 4x - 1)² - 16 ≥ - 16
- Khi x = 0 ⇒ y = - 15
- Khi x = 1 ⇒ y = 0
- Khi x² + 4x - 1 = 0 ⇔ x = √5 - 2 ( loại giá trị x = - √5 - 2 < 0) ⇒ y = - 16
Vậy trên đoạn [0; 1] thì :
GTNN của y = - 16 khi x = √5 - 2
GTLN của y = 0 khi x = 1

Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

Lời giải:
$x^2-2x-3=x(x+3)-5(x+3)+12=(x+3)(x-5)+12$
Vì $x\in [-3;4]$ nên $x+3\geq 0; x-5< 0$
$\Rightarrow x^2-2x-3=(x+3)(x-5)+12\leq 12$
Vậy GTLN của hàm số là $12$ khi $x=-3$
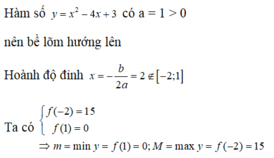
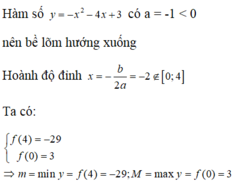
mk làm 1 câu còn mấy câu còn lại bn làm tương tự cho quen nha .
ta có : \(2x^2+4x-7=2x^2+4x+2-9=2\left(x+1\right)^2-9\)
vì \(x\in\left[-3;4\right]\)\(\Rightarrow50\ge2\left(x+1\right)^2-9\ge-9\)
\(\Rightarrow y_{min}=-9\) khi \(x=-1\) và \(y_{max}=50\) khi \(x=4\)
vậy ...................................................................................................................
vì sao mak ra sô 50 vậy bn