Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=FE

Lời giải:
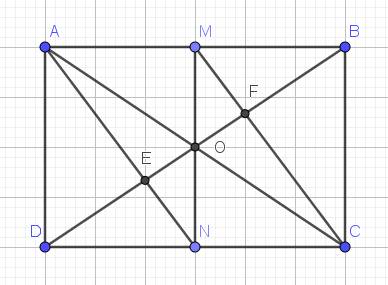
a. Vì $ABCD$ là hình chữ nhật nên $\widehat{A}=\widehat{D}=90^0$
$MN\perp CD$ nên $\widehat{MND}=90^0$
Tứ giác $AMND$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{N}$ nên là hcn.
b.
Hoàn toàn tương tự phần a ta thấy $\widheat{B}=\widehat{C}=\widehat{N}$ nên $BMNC$ là hcn
$\Rightarrow BM=NC$
$AMND$ là hcn nên $AM=DN$
Mà $AM=BM$ nên $AM=NC$
Có $AM\parallel NC$ (do $AB\parallel CD$) và $AM=NC$ nên $AMCN$ là hbh
$\Rightarrow AC, MN$ cắt nhau tại trung điểm mỗi đường.
Mà $O$ là trung điểm $MN$ nên $O$ cũng là trung điểm $AC$.
c.
Vì $AMCN$ là hbh (theo phần b) nên $AN\parallel CM$
$\Rightarrow EN\parallel FC$
$\Rightarrow \frac{DE}{EF}=\frac{DN}{NC}=1$ (theo định lý Talet)
$\Rightarrow DE=EF(1)$
Mặt khác:
$AN\parallel CM$
$\Rightarrow MF\parallel AE$
$\Rightarrow \frac{BF}{EF}=\frac{BM}{MA}=1$ (định lý Talet)
$\Rightarrow BF=EF(2)$
Từ $(1); (2)\Rightarrow DE=EF=BF$
câu 1:
\(B=\dfrac{x-2}{y}-\dfrac{x}{x-2}+\dfrac{4}{x.\left(x-2\right)}\)
\(\Leftrightarrow B=\dfrac{\left(x-2\right)^2.x}{y.\left(x-2\right).x}-\dfrac{x^2y}{y.\left(x-2\right).x}+\dfrac{4y}{y.\left(x-2\right).x}\)
\(\Leftrightarrow B=\dfrac{\left(x-2\right)^2-x^2y+4y}{x^2y-2xy}\)
\(\Leftrightarrow B=\dfrac{\left(x-2\right)^2-y.\left(x^2-4\right)}{xy.\left(x-2\right)}\)
\(\Leftrightarrow B=\dfrac{\left(x-2\right)^2-y.\left(x-2\right).\left(x+2\right)}{xy.\left(x-2\right)}\)
\(\Leftrightarrow B=\dfrac{\left(x-2\right)\left[x-2-y.\left(x+2\right)\right]}{xy.\left(x-2\right)}\)
\(\Leftrightarrow B=\dfrac{x-2-xy+2}{xy}=\dfrac{x-xy}{xy}\)
\(\Leftrightarrow B=\dfrac{x}{xy}-\dfrac{xy}{xy}=\dfrac{1}{y}-1=\dfrac{1-y}{y}\)
Vậy \(B=\dfrac{1-y}{y}\)
a) Xét tứ giác AEFD có:
\(\widehat{EAD}=\widehat{ADF}=\widehat{EFD}\) (cùng bằng 90 độ)
=> AEFD là hình chữ nhật (do có 3 góc vuông)
Gọi I' là 1 điểm mà AC cắt EF
Xét tam giác CAD có:
I' nằm trên EF nêm I'F song song với AD (AEFD là hình chữ nhật) (1)
vì AEFD là hình chữ nhật nên AE=DF => DF = DC :2 <=> F là trung điểm của CD (2)
Từ (1) và (2) => I' là trung điểm của AC đồng thời ta được I'F = AD:2
mà AD = EF
=> I' là trung điểm của EF => I' trùng với I
=> I là trung điểm của AC
( do I' là trung điểm của AC và I' là giao điểm của AC và EF)
=> điều phải chứng minh