Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

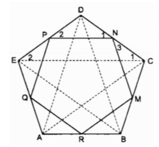
Xét △ ABC và △ BCD:
AB = BC (gt)
∠ B = ∠ C (gt)
BC = CD (gt)
Do đó: △ ABC = △ BCD (c.g.c)
⇒ AC = BD (1)
Xét △ BCD và △ CDE:
BC = CD (gt)
∠ C = ∠ D (gt)
CD = DE (gt)
Do đó: △ BCD = △ CDE (c.g.c) ⇒ BD = CE (2)
Xét △ CDE và △ DEA:
CD = DE (gt)
∠ D = ∠ E (gt)
DE = EA (gt)
Do đó: △ CDE = △ DEA (c.g.c) ⇒ CE = DA (3)
Xét △ DEA và △ EAB:
DE = EA (gt)
∠ E = ∠ A (gt)
EA = AB (gt)
Do đó: △ DEA = △ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong △ ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong △ CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong △ DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong △ EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ((5-2 ). 180 0 )/5 = 108 0
△ DPN cân tại D
⇒ ∠ (DPN) = ∠ (DNP) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
△ CNM cân tại C
⇒ ∠ (CNM) = ∠ (CMN) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (ADN) + ∠ (PNM) + ∠ (CNM) = 180 0
⇒ ∠ (PNM) = 180 0 - ( ∠ (ADN) + ∠ (CNM) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ BMR cân tại B
⇒ ∠ (BMR) = ∠ (BRM) = ( 180 0 - ∠ B )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (CMN) + ∠ (BRM) + ∠ (BMR) = 180 0
⇒ ∠ (NMR) = 180 0 - ( ∠ (CMN) + ∠ (BMR) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ ARQ cân tại A
⇒ ∠ (ARQ) = ∠ (AQR) = ( 180 0 - ∠ A )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (BRM) + ∠ (MRQ) + ∠ (ARQ) = 180 0
⇒ ∠ (MRQ) = 180 0 - ( ∠ (BRM) + ∠ (ARQ) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ QEP cân tại E
⇒ ∠ (EQP) = ∠ (EPQ) = ( 180 0 - ∠ E )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (AQR) + ∠ (RQP) + ∠ (EQP) = 180 0
⇒ ∠ (RQP) = 180 0 - ( ∠ (AQR) + ∠ (EQP) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
∠ (EQP) + ∠ (QPN) + ∠ (DPN) = 180 0
⇒ ∠ (QPN) = 180 0 - ( ∠ (EPQ) + ∠ (DPN) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
Suy ra : ∠ (PNM) = ∠ (NMR) = ∠ (MRQ) = ∠ (RQP) = ∠ (QPN)
Vậy MNPQR là ngũ giác đều.

cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.