Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều dương là chiều chuyển động của viên đạn
ÁP dụng định luật bảo toàn động lượng ta có:
\(m_2v_2cos60-m_1v_1=0=>v_2=\dfrac{m_1v_1}{m_2cos60}=\dfrac{7500.1}{20.cos60}=750(m/s)\)
=> Chọn B

Chọn C.
Chọn hệ trục Ox như hình vẽ
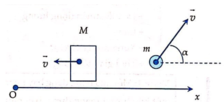
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox
![]()
Vì trước khi bắn hệ đứng yên
Chiếu phương trình (*) lên Ox ta được: 0 = -p’1 + p’2.cos60o
Thay số ta được:
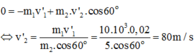

Chọn C.
Chọn hệ trục Ox như hình vẽ
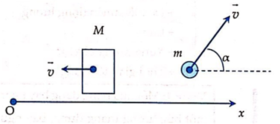
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox


Phương trình bảo toàn vecto động lượng cho hệ theo Ox ( Vì theo Ox khi hợp lực tác dụng vào vật theo phương Ox bị triệt tiêu ) O---------->x
\(\overrightarrow{0}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Vì trước khi bắn hệ đứng yên: Chiếu phương trình lên trục Ox ta được: \(0=-p_1+p_2\cos\left(60^0\right)\) Thay số:
\(0=-m_1v_1+m_2v_2\cos\left(60^0\right)\Rightarrow v_2=\dfrac{m_1v_1}{m_2\cos\left(60^0\right)}\) Thay số nốt hộ mình là ra :D

Chiều (+) là chiều CĐ của đạn:
a. Toa xe đứng yên v = 0 p = 0
Theo định luật bảo toàn động lượng ta có:
( m 1 + m 2 + m 3 ) v = ( m 1 + m 2 ) v / + m 3 v 0 ⇒ v / = ( m 1 + m 2 + m 3 ) v − m 3 . v 0 m 1 + m 2 = 0 − 1.400 130 + 20 ≈ − 2 , 67 m / s
Toa xe CĐ ngược chiều với chiều viên đạn
b. Theo định luật bảo toàn động lượng ta có:
( m 1 + m 2 + m 3 ) v 1 = ( m 1 + m 2 ) v / + m 3 ( v 0 + v 1 ) ⇒ v / = ( m 1 + m 2 + m 3 ) v 1 − m 3 . ( v 0 + v 1 ) m 1 + m 2 ⇒ v / = ( 130 + 20 + 1 ) .5 − 1. ( 400 + 5 ) 130 + 20 ≈ 2 , 33 ( m / s )
Toa xe CĐ theo chiều bắn nhưng vận tốc giảm đi.
c. Theo định luật bảo toàn động lượng ta có
− ( m 1 + m 2 + m 3 ) v 1 = ( m 1 + m 2 ) v / + m 3 ( v 0 − v 1 ) ⇒ v / = − ( m 1 + m 2 + m 3 ) v 1 − m 3 . ( v 0 − v 1 ) m 1 + m 2 ⇒ v / = − ( 130 + 20 + 1 ) .5 − 1. ( 400 − 5 ) 130 + 20 ≈ − 7 , 67 ( m / s )
Vận tốc của toa vẫn theo chiều cũ và tăng tốc.

+ Theo định luật bảo toàn động lượng:
− m 1 + m 2 + m 3 v 1 = m 1 + m 2 v / + m 3 v 0 − v 1
⇒ v / = − m 1 + m 2 + m 3 v 1 − m 3 v 0 − v 1 m 1 + m 2 = − 130 + 20 + 1 .5 − 1 400 − 5 130 + 20 ≈ − 7 , 67 m / s
+ Vận tốc của toa vẫn theo chiều cũ và tăng tốc.
Chọn đáp án B

+ Theo định luật bảo toàn động lượng:
m 1 + m 2 + m 3 v 1 = m 1 + m 2 v / + m 3 v 0 + v 1
⇒ v / = m 1 + m 2 + m 3 v 1 − m 3 v 0 + v 1 m 1 + m 2 = 130 + 20 + 1 .5 − 1 400 + 5 130 + 20 ≈ 2 , 33 m / s
+ Toa xe chuyển động theo chiều bắn nhưng vận tốc giảm đi
Chọn đáp án D

Chọn chiều chuyển động của viên đạn là chiều dương. Hệ vật gồm bệ pháo, khẩu pháo và viên đạn. Gọi V 0 và V là vận tốc của bộ pháo trước và sau khi bắn, còn v là vận tốc đầu nòng của viên đạn. Vì các phần của hệ vật đều chuyển động theo cùng phương ngang, nên có thể biểu diễn tổng động lượng của hệ vật này dưới dạng tổng đại số.
Trước khi bắn : p 0 = ( M 1 + M 2 + m) V 0
Sau khi bắn : p = ( M 1 + M 2 )V + m(v + V).
Áp dụng định luật bảo toàn động lượng :
p = p 0 ⇒ ( M 1 + M 2 )V + m(v + V) = ( M 1 + M 2 + m) V 0
suy ra : V = (( M 1 + M 2 + m) V 0 - mv)/( M 1 + M 2 + m)
trong đó V 0 , V, v là giá trị đại số của các vận tốc đã cho.
Trước khi bắn, nếu bệ pháo đứng yên ( V 0 = 0 ), thì ta có :
V = -mv/(M1 + M2 + m) = -100.500/15100 = -3,3(m/s)

Lúc đầu hệ vật đứng yên có động lượng p 0 = 0. Ngay sau khi bắn, hệ vật có động lượng MV + mv = 0. Áp dụng định luật bảo toàn động lượng cho chuyển động theo phương ngang của hệ vật ta có:
p = p 0 ⇒ MV + mv = 0
suy ra MV = - mv hay V = -mv/M = -10.800/10000 = -0,8(m/s)
Câu 1.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1\cdot v_1+m_2\cdot v_2=\left(m_1+m_2\right)\cdot V\)
\(\Rightarrow2000\cdot30+3000\cdot40=\left(2000+3000\right)\cdot V\)
\(\Rightarrow V=36\)m/s
Câu 2.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{0}\)
\(\Rightarrow-p_1+p_2=0\)
\(\Rightarrow p_1=p_2\Rightarrow m_1\cdot v_1=m_2\cdot v_2\)
\(\Rightarrow7500\cdot1=20\cdot v_2\)
\(\Rightarrow v_2=375\)m/s