Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Liên Giải thích đúng vì nếu theo Oanh thì so sánh 2/8 <1/2 mà theo Oanh là 2 > 1 ; 8 > 2 suy ra 2/8 > 1/2 là sai

Theo phương pháp so sánh hai phân số có cùng mẫu số mà chúng ta đã được học thì bạn Liên giải thích đúng, còn Oanh giải thích sai.
Ví dụ cho thấy bạn Oanh sai : hai phân số 3/8 và 1/2 có 3 lớn hơn 1 còn 8 lớn hơn 2 nhưng 3/8 nhỏ hơn 1/2 vì khi quy đồng về mẫu số chung là 8 thì ta có: 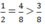

Sao nhiều quá vại??
mk lm k nổi đâu
Dài quá nhìn lòi bảng họng lun ak
Bài : 4
a/ \(\frac{1}{5\cdot6}+\frac{1}{6\cdot7}+\frac{1}{7\cdot8}+....+\frac{1}{24\cdot25}\)
\(=\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+....+\frac{1}{24}-\frac{1}{25}\)
\(=\frac{1}{5}-\frac{1}{25}\)
\(=\frac{4}{25}\)
b/ \(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+\frac{2}{5\cdot7}+....+\frac{2}{99\cdot101}\)
\(=\frac{3-1}{1\cdot3}+\frac{5-3}{3\cdot5}+\frac{7-5}{5\cdot7}+...+\frac{101-99}{99\cdot101}\)
\(=\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{99}-\frac{1}{101}\)
\(=\frac{1}{1}-\frac{1}{101}\)
\(=\frac{100}{101}\)
c/ \(\frac{5^2}{1\cdot6}+\frac{5^2}{6\cdot11}+\frac{5^2}{11\cdot16}+\frac{5^2}{16\cdot21}+\frac{5^2}{21\cdot26}+\frac{5^2}{26\cdot31}\)
\(=\frac{25}{1\cdot6}+\frac{25}{6\cdot11}+\frac{25}{11\cdot16}+\frac{25}{16\cdot21}+\frac{25}{21\cdot26}+\frac{25}{26\cdot31}\)
\(=\frac{6-1}{1\cdot6}+\frac{11-6}{6\cdot11}+....+\frac{31-26}{26\cdot31}\)
\(=\frac{25}{5}\cdot\left(\frac{1}{1}-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+....+\frac{1}{26}-\frac{1}{31}\right)\)
\(=\frac{25}{5}\cdot\left(\frac{1}{1}-\frac{1}{31}\right)\)
\(=\frac{25}{5}\cdot\frac{30}{31}\)
\(=\frac{150}{31}\)
d/ \(\frac{3}{1\cdot3}+\frac{3}{3\cdot5}+\frac{3}{5\cdot7}+....+\frac{3}{49\cdot51}\)
\(=\frac{3-1}{1\cdot3}+\frac{5-3}{3\cdot5}+\frac{7-5}{5\cdot7}+....+\frac{51-49}{49\cdot51}\)
\(=\frac{3}{2}\cdot\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{49}-\frac{1}{51}\right)\)
\(=\frac{3}{2}\cdot\left(\frac{1}{1}-\frac{1}{51}\right)\)
\(=\frac{3}{2}\cdot\frac{50}{51}\)
\(=\frac{25}{17}\)
e/ \(\frac{1}{7}+\frac{1}{91}+\frac{1}{247}+\frac{1}{475}+\frac{1}{775}+\frac{1}{1147}\)
\(=\frac{1}{1\cdot7}+\frac{1}{7\cdot13}+\frac{1}{13\cdot19}+\frac{1}{19\cdot25}+\frac{1}{25\cdot31}+\frac{1}{31\cdot37}\)
\(=\frac{7-1}{1\cdot7}+\frac{13-7}{7\cdot13}+....+\frac{37-31}{31\cdot37}\)
\(=\frac{1}{6}\cdot\left(1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+....+\frac{1}{31}-\frac{1}{37}\right)\)
\(=\frac{1}{6}\cdot\left(1-\frac{1}{37}\right)\)
\(=\frac{1}{6}\cdot\frac{36}{37}\)
\(=\frac{6}{37}\)

A) \(\frac{1}{2}\cdot\left(\frac{2}{9}+\frac{3}{7}-\frac{5}{27}\right)\)
\(=\frac{1}{2}\cdot\frac{1}{2}\)
\(=\frac{1}{4}\)
B) \(\left(\frac{-5}{28}+1.75+\frac{8}{35}\right):\left(-3\frac{9}{20}\right)\)
\(=\left(\frac{-5}{28}+\frac{7}{4}+\frac{8}{35}\right):\frac{-69}{20}\)
\(=\frac{14}{5}:\frac{-69}{20}\)
\(=\frac{-56}{69}\)

\(a)\frac{\left(\frac{3}{10}-\frac{4}{15}-\frac{7}{20}\right).\frac{5}{19}}{\left(\frac{1}{14}+\frac{1}{7}-\frac{-3}{35}\right).\frac{-4}{3}}\)\(=\frac{\frac{-19}{60}.\frac{5}{19}}{\frac{3}{10}.\frac{-4}{3}}=\frac{5}{24}\)
Hok tốt
theo tui thì Liên đúng vì khi so sánh 2 phân số khác mẫu ta fai quy đồng trước khi so sánh