Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Sai số tuyệt đối (MAD) và sai số tỷ đối (MAPE) được tính như sau:
Phép đo thực tế (TTT): 200,1mm, 200mm, 199mm, 200,05mm, 199,05mm
Phép đo lý thuyết (TDT): 200mm, 200mm, 200mm, 200mm, 200mm, 200mm
MAD = |(TTT - TDT)| = |(200,1 - 200), (200 - 200), (199 - 200), (200,05 - 200), (199,05 - 200)| = (0,1), 0, 1, 0, 1, 1 mm
MAPE = |(TTT - TDT)/TTT)|*100 = |(200,1 - 200)/200,1), (200 - 200)/200), (199 - 200)/199), (200,05 - 200)/200,05), (199,05 - 200)/199,05)|*100 = 0,05%, 0%, 0,05%, 0,05%, 0,05%
b. Kết quả phép đo:
Độ lỗi tuyệt đối tối đa: 1,1 mm (từ 0,1 mm tới 1,1 mm)Độ lỗi tỷ đối tối đa: 0,05% (từ 0% tới 0,05%)Vậy độ lỗi tuyệt đối và tỷ đối tối đa của phép đo đo chiều dài quyển sách 5 lần là:
Độ lỗi tuyệt đối tối đa: 1,1 mmĐộ lỗi tỷ đối tối đa: 0,05%
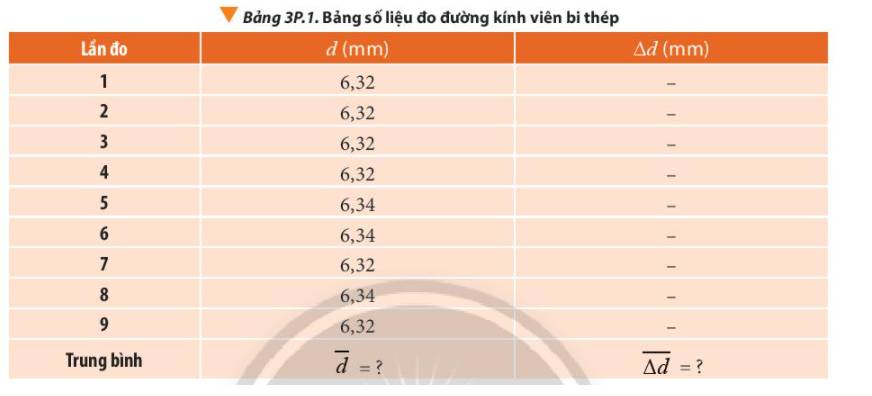
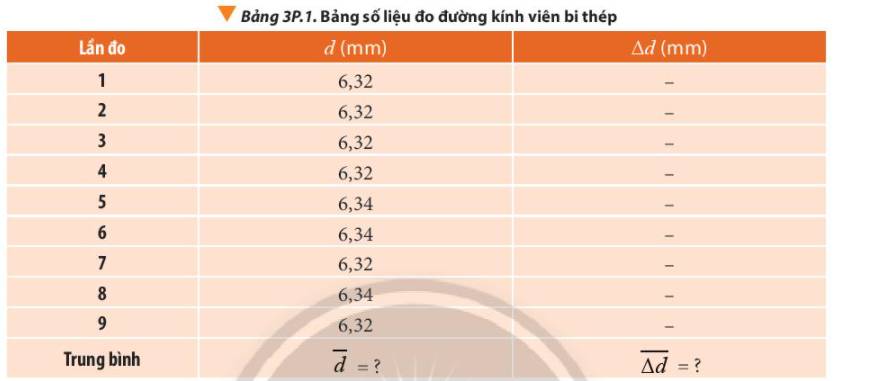
Giá trị trung bình của đường kính viên bi thép là:
\(\overline d = \frac{{{d_1} + {d_2} + ... + {d_9}}}{9} \approx 6,33(mm)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {d_1} = \left| {\overline d - {d_1}} \right| = \left| {6,33 - 6,32} \right| = 0,01(mm) = \Delta {d_2} = \Delta {d_3} = \Delta {d_4} = \Delta {d_7} = \Delta {d_9}\\\Delta {d_5} = \left| {\overline d - {d_5}} \right| = \left| {6,33 - 6,34} \right| = 0,01(mm) = \Delta {d_6} = \Delta {d_8}\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_9}}}{9} = 0,01(mm)\)
Sai số tuyệt đối của phép đo là:
\(\Delta d = \overline {\Delta d} + \Delta {d_{dc}} = 0,01 + 0,02 = 0,03(mm)\)

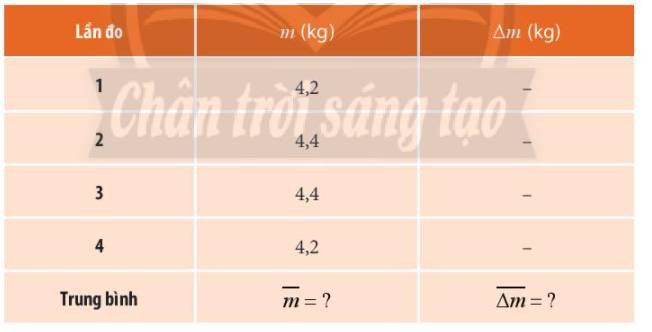
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)

a) Nhờ bạn bấm máy tính kiểm tra nhé.
Giá trị trung bình của l:
\(\overline{l}=\frac{l_1+l_2+..+l_n}{n}=\frac{50+52+51+51+50}{5}=50,8\)
b) Sai số tuyệt đối \(\Delta A_1=\left|\overline{A}-A_1\right|;\Delta A_2=\left|\overline{A}-A_2\right|\)
Khi đó sai số tuyệt đối ở mỗi lần đo là
\(\Delta l_1=\left|\overline{I}-I_1\right|=\left|50,8-50\right|=0,8.\)
Tương tự cho 4 lần đo tiếp theo.
c) Sai số tuyệt đối trung bình
\(\overline{\Delta I}=\frac{\Delta I_1+\Delta I_2+..+\Delta I_5}{5}=...\)
d) Sai số tuyệt đối của phép đo \(\Delta l=\overline{\Delta l}+\Delta l'=\overline{\Delta l}+\frac{1}{2}\)số chia nhỏ nhât = ....
e) Sai số tỉ đối \(\delta l=\frac{\Delta l}{\overline{l}}.100\%\)

Câu 5: Dùng một thước chia độ nhỏ nhất đến milimét để đo khoảng cách l giữa hai điểm A, B và có kết quả đo là 600 mm. Lấy sai số dụng cụ là một độ chia nhỏ nhất. Cách ghi nào sau đây không đúng với số chữ số có nghĩa của phép đo?
A. ℓ = (6,00 ± 0,01) dm. B. ℓ = (0,6 ± 0,001) m.
C. ℓ = (60,0 ± 0,1) cm. D. ℓ = (600 ± 1) mm.



a. Sai số tuyệt đối và sai số tỷ đối:
Ta tính tổng độ sai số của các giá trị đo lượng thực như sau:
Sai sốĐộ sai số
Tổng độ sai số = 0 + 0 + 1 + 5 + 1 = 7
Giá trị thực là 550mm, vậy sai số tuyệt đối = |550 - 500| = 100.
Tỷ đối sai số = (7/1000) x 100 = 0.7%.
b. Kết quả phép đo:
Sai số tuyệt đối: 100mmSai số tỷ đối: 0.7%Vậy kết quả phép đo của chiều dài quyển sổ là 550mm với sai số tuyệt đối là 100mm và sai số tỷ đối là 0.7%.