Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

tham khảo:

Gọi I là trung điểm của BD.
Tam giác BCD có IM là đường trung bình nên IM//DC và IM=\(\dfrac{1}{2}\)CD=\(\dfrac{1}{2}\).2a=1
Tam giác ABD có IN là đường trung bình nên IN//AB và IN=\(\dfrac{1}{2}\)AB=\(\dfrac{1}{2}\).2a=1
Ta có: cos\(\widehat{MIN}\)=\(\dfrac{a^2+a^2-\left(a\sqrt{3}\right)^2}{2.a.a}=\dfrac{-1}{2}\)
Nên \(\widehat{MIN}\)=\(120^0\)
Do AB//IN, CD//IM nên góc giữa AB và CD là góc giữa IM và IN là bằng \(120^0\)

1. Câu này đề bài là: \(\lim\limits_{x\rightarrow1}\dfrac{x-\sqrt[]{x+2}}{x-\sqrt[3]{3x+2}}\) đúng ko nhỉ?
Vậy thay số là được: \(=\dfrac{1-\sqrt[]{1+2}}{1-\sqrt[3]{3+2}}=\dfrac{1-\sqrt[]{3}}{1-\sqrt[3]{5}}\)
2.
a. \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
b.
Trong mp (ABCD), từ D kẻ \(DE\perp AC\) (1)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp DE\) (2)
(1);(2) \(\Rightarrow DE\perp\left(SAC\right)\Rightarrow SE\) là hình chiếu vuông góc của SD lên (SAC)
\(\Rightarrow\widehat{DSE}\) là góc giữa SD và (SAC) hay \(\widehat{DSE}=\alpha\)
\(AC=\sqrt{AB^2+AD^2}=a\sqrt{5}\)
Áp dụng hệ thức lượng trong tam giác vuông ADC:
\(AE.AC=AD^2\Rightarrow AE=\dfrac{AD^2}{AC}=\dfrac{4a\sqrt{5}}{5}\)
\(SE=\sqrt{SA^2+AE^2}=\dfrac{a\sqrt{105}}{5}\) ; \(SD=\sqrt{SA^2+AD^2}=a\sqrt{5}\)
\(\Rightarrow cos\alpha=\dfrac{SE}{SD}=\dfrac{\sqrt{21}}{5}\)

Đáp án A
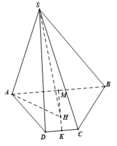
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) ![]()

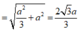
![]()
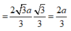
![]()
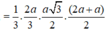
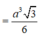
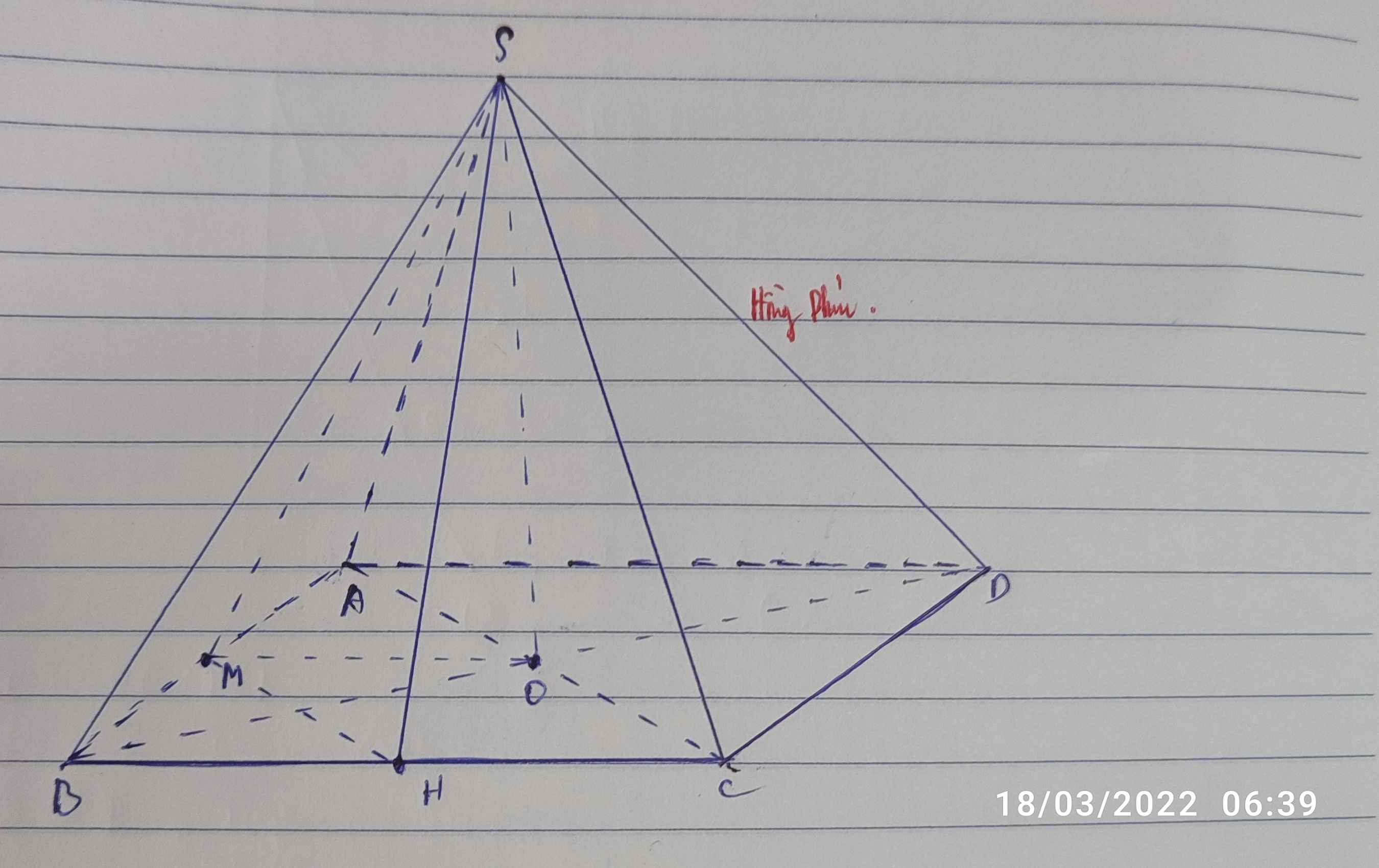

Câu 8:
Kẻ \(AH\perp SM\)
Trong mặt phẳng (SBC), qua H kẻ đường thẳng song song BC cắt SB và SC lần lượt tại P và Q
\(\Rightarrow\Delta APQ\) là thiết diện của (P) và chóp
\(AM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow SA=AM\Rightarrow\Delta SAM\) vuông cân tại A
\(\Rightarrow AH=\frac{SA\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\) đồng thời H là trung điểm SM
\(\Rightarrow PQ=\frac{1}{2}BC=\frac{a}{2}\) (đường trung bình)
\(\Rightarrow S_{\Delta APQ}=\frac{1}{2}AH.PQ=\frac{a^2\sqrt{6}}{16}\)
Câu 9.
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=AH=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAH\) vuông cân tại H
\(\Rightarrow\widehat{SAH}=45^0\)
Câu 6:
Bạn kiểm tra lại đề, \(SO\perp\left(ABCD\right)\Rightarrow SO\perp OB\Rightarrow\widehat{SOB}=90^0\)
Nên không thể có chuyện \(tan\widehat{SOB}=\frac{1}{2}\)
Câu 7:
H là trực tâm tam giác ABC \(\Rightarrow BH\perp AC\)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
K là trực tâm tam giác SBC \(\Rightarrow BK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BHK\right)\Rightarrow\) góc giữa SC và (BHK) bằng 90 độ