Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{Câu 1 : Tự tính}\)
\(\text{Câu 2:a)Cho x = 1 ;ta có : y = 3.1 = 3}\)
\(\text{Lấy điểm A (}1;3)\)
3. Gọi a,b,c là số tiền lãi của mỗi người \((\text{triệu đồng})\)
Theo đề bài , ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\text{ và }a+b+c=105(\text{triệu})\)
\(\text{Áp dụng tính chất dãy tỉ sô bằng nhau , ta có :}\)
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{105}{15}=7\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{3}=7\\\frac{b}{5}=7\\\frac{c}{7}=7\end{cases}}\Rightarrow\hept{\begin{cases}a=21(\text{triệu})\\b=35(\text{triệu})\\c=49(\text{triệu})\end{cases}}\)
Vậy
\(\text{Bài 4,5 : Bạn tự làm nhé }\)
Chúc bạn học tốt :>

A) XÉT \(\Delta ABM\) VÀ \(\Delta DCM\) CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{BMA}=\widehat{CMD}\left(Đ^2\right)\)
\(AM=DM\left(GT\right)\)
=>\(\Delta ABM\)=\(\Delta DCM\)(C-G-C)
B)VÌ =>\(\Delta ABM\)=\(\Delta DCM\)(CMT)
=>\(\widehat{BAM}=\widehat{MDC},HAY,\widehat{BAD}=\widehat{ADC}\)
HAI GÓC BAD VÀ ADC Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
=>AB//DC
C) XÉT HAI TAM GIÁC VUÔNG \(\widehat{BEM}\)VÀ\(\widehat{CFM}\)CÓ
\(\widehat{BME}=\widehat{CMF}\left(Đ^2\right)\)
\(BM=CM\left(GT\right)\)
=>\(\widehat{BEM}\)=\(\widehat{CFM}\)( CẠNH HUYỀN - GÓC NHỌN )
=> EM = FM(1)
VÀ M NẰM GIỮA A VÀ F (2)
TỪ 1 VÀ 2 => M LÀ TRUNG ĐIỂM CỦA AF

Câu 3:
a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
c: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó ΔBME=ΔCMF
Suy ra: ME=MF
hay M là trung điểm của FE

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF

a) Xét ΔABM và ΔDCM có:
BM=CM(gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM=DM(gt)
=>ΔABM=ΔDCM(c.g.c)
b) Vì ΔABM=ΔDCM(cmt)
=>\(\widehat{ABM}=\widehat{DCM}\). Mà hai góc này pử vị trí sole trong
=>AB//DC
c)Xét ΔEBM và ΔFCM có:
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM=MC(gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
=>ΔEBM=ΔFCM( cạnh huyền-góc nhọn)
=>ME=MF
=>M là trung điểm của EF
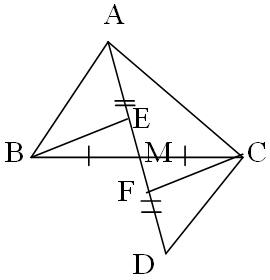
a) Xét ΔABM và ΔDCM, có:
MB = MC (gt)
∠AMB = ∠DCM (đối đỉnh)
MA = MD (gt)
Vậy ΔABM = ΔDCM (c-g-c)
b) Từ ΔABM = ΔDCM (chứng minh câu a)
Suy ra: ∠ABM = ∠ DCM (hai góc tương ứng)
Mà hai góc ∠ABM và ∠DCM ở vị trí so le trong
Vậy AB // DC
c) Xét ΔBEM và ΔCFM (∠E = ∠F = 90º)
Có: MB = MC (gt)
∠AMB = ∠DMC (đối đỉnh)
Do đó: ΔBEM = ΔCFM (cạnh huyền-góc nhọn)
Suy ra: ME = MF (hai cạnh tương ứng)
Vậy M là trung điểm của EF

a ) Xét \(\Delta ABM\)và \(\Delta DCB\) có :
BM = CM (gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM = DM (gt)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
Vì : \(\Delta ABM=\Delta DCM\left(cmt\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) . Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AB // DC
c ) Xét \(\Delta EBM\) và \(\Delta FCM\) có :
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM = MC (gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
\(\Rightarrow\Delta EBM=\Delta FCM\)(cạnh huyền - góc nhọn )
\(\Rightarrow ME=MF\)
\(\Rightarrow M\) là trung điểm của EF ( đpcm)
Chúc bạn học tốt !!!

4:
b: Xét tứ gác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//CD

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: ta có: ΔABM=ΔDCM
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét ΔMEB vuông tại E và ΔMFC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔMEB=ΔMFC
=>ME=MF
mà M nằm giữa E và F
nên M là trung điểm của EF
bài 4
a)xét tam giác ABM và tam giác DCM có
BM=CM( là trung điểm của BC)
AM=DM( gt)
\(\widehat{AMB}\)=\(\widehat{DMC}\)(đối đỉnh)
do đó : tam giác ABM= tam giác DCM(c.g.c)
b)do tam giác ABM= tam giác DCM nên \(\widehat{ABM}\)= \(\widehat{DCM}\)
Mà 2 góc này ở vị trí so le trong nên AB song song CD
c) xét tam giác BME và tam giác CMF có
BM=CM ( M là trung điểm của BC)
\(\widehat{BME}\)=\(\widehat{DMF}\)( đối đỉnh)
\(\widehat{BEM}\)=\(\widehat{DFM}\)=90 độ
do đó tam giác BME= tam giác DFM( cạnh huyền -góc nhọn)
=> ME=MF
mà M,E,F thẳng hàng (E thuộc AM, F thuộc DM hay F thuộc AM)
=> M là trung điểm của EF
mệt chết đc
nhớ ủng hộ mk đó