Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
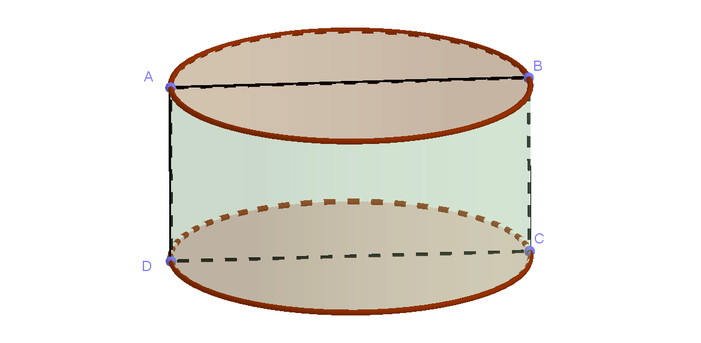
Chọn B.
Phương pháp:
Thiết diện qua trục của hình trụ có bán kính đáy R và chiều cao h là hình chữ nhật có kích thước 2R × h. Thể tích khối trụ bán kính đáy R và chiều cao h là V = πR 2 h .
Cách giải:
Một mặt phẳng qua trục cắt khối trụ theo thiết diện là một hình chữ nhật có diện tích bằng 16a2
⇒ 2 R . 2 R = 16 a 2 ⇔ R 2 = 4 a 2 ⇔ R = 2 a ⇒ h = 2 R = 4 a
Thể tích của khối trụ đã cho: V = πR 2 h = π . ( 2 a ) 2 . 4 a = 16 πa 3 .
Đáp án A
2 π R = 4 R + 2 h ⇒ h = R ( π − 2 ) ⇒ S x q S t p = 2 π R h 2 π R h + 2 π R 2 = π − 2 π − 1
S A B C D = 8 a 2 ⇒ 2 a . h = 8 a 2 ⇔ h = 4 a
Diện tích xung quanh của hình trụ:
S x q = 2 πRh = 2 π . a . 4 a = 8 πa 2
Thể tích khối trụ
V t r ụ = πR 2 h = πa 4 . 4 a = 4 πa 3
Chọn đáp án C.
Đáp án C
Phương pháp:
Diện tích xung quanh của hình trụ 
và thể tích khối trụ 
Cách giải: Mặt phẳng qua trục cắt hình trụ theo thiết diện là hình chữ nhật có một cạnh là đường kính đáy và một cạnh là chiều cao của hình lăng trụ.
Gọi h là chiều cao của hình trụ ta có 
Vậy diện tích xung quanh của hình trụ 
và thể tích khối trụ
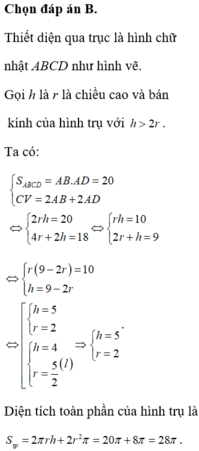
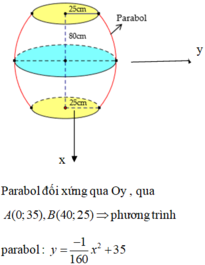
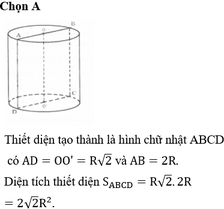
Đáp án là C