Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\int\limits^2_0\left[f\left(x\right)-2g\left(x\right)\right]dx=\int\limits^2_0f\left(x\right)dx-2\int\limits^2_0g\left(x\right)dx=3+2=5\)

\(A=log_m\left(8m\right)=log_mm+log_m8\)
\(=1+log_m8\)
\(=1+\dfrac{1}{log_8m}=1+\dfrac{1}{log_{2^3}m}=1+\dfrac{1}{\dfrac{1}{3}\cdot log_2m}\)
\(=1+\dfrac{1}{\dfrac{1}{3}a}=1+1:\dfrac{a}{3}=1+\dfrac{3}{a}=\dfrac{a+3}{a}\)
=>Chọn A

|
1 |
B |
6 |
B |
11 |
C |
16 |
A |
21 |
D |
|
2 |
C |
7 |
A |
12 |
A |
17 |
B |
22 |
D |
|
3 |
A |
8 |
B |
13 |
B |
18 |
C |
23 |
C |
|
4 |
B |
9 |
B |
14 |
A |
19 |
A |
24 |
A |
|
5 |
D |
10 |
C |
15 |
D |
20 |
D |
25 |
C |

Cách tính bài này đơn giản là tọa độ hóa nó (tứ diện cần tính ko đặc biệt, nhưng chóp ban đầu thì tọa độ hóa được), gọi A là gốc (0,0,0), quy ước a là 1 đơn vị độ dài, các tia AS, AB, AD lần lượt là Oz, Oy, Ox, ta có các tọa độ \(S\left(0,0,1\right)\); M(1,0,0), D(2,0,0), C(2,1,0), \(I\left(x;y;z\right)\) là tâm
\(SI=CI=DI=MI\Rightarrow\left\{{}\begin{matrix}x^2+y^2+\left(z-1\right)^2=\left(x-1\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+y^2+z^2\\x^2+y^2+\left(z-1\right)^2=\left(x-2\right)^2+\left(y-1\right)^2+z^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-z=0\\4x-2z=3\\4x+2y-2z=4\end{matrix}\right.\) \(\Rightarrow I\left(\dfrac{3}{2};\dfrac{1}{2};\dfrac{3}{2}\right)\)
\(\Rightarrow R=SI=\dfrac{\sqrt{11}}{2}\)
Do quy ước a là 1 đơn vị độ dài nên đáp án chính xác là \(R=\dfrac{a\sqrt{11}}{2}\)
Lý do đáp án chỉ có số mà thiếu a: theo tư duy của mình thì người ra đề mang hướng giải y như mình bên trên, tức là quy ước độ dài rồi tọa độ hóa, nhưng khi đưa ra đáp án cuối cùng lại quên chuyển từ quy ước về đơn vị thực nên thiếu a. Về cơ bản là người ta quên, ko có gì bí ẩn đáng suy nghĩ ở đây cả :D. Kích thước là a thì mọi kích thước độ dài sẽ phụ thuộc a.





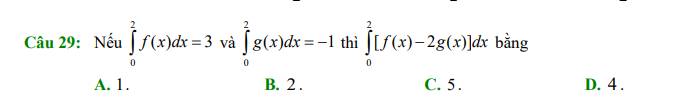

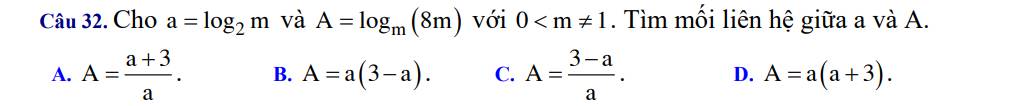


Mã đề 118
Mã đề 101