Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có:
\(5^2+\left(a-1\right)^2=a^2\)
\(\Leftrightarrow a^2=a^2-2a+1+25\)
=>a=13

Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 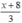 (m)
(m)
Tam giác vuông mới có diện tích bằng 51 m 2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
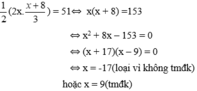
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

Gọi độ dài cạnh góc vuông thứ 2 là x>0 (cm)
\(\Rightarrow\) Độ dài cạnh huyền là \(x+2\) (cm)
Theo định lý Pitago ta có:
\(4^2+x^2=\left(x+2\right)^2\)
\(\Leftrightarrow16+x^2=x^2+4x+4\)
\(\Leftrightarrow4x=12\Rightarrow x=3\)
Vậy độ dài cạnh huyền là \(3+2=5\left(cm\right)\)

1/ Gọi chiều dài hình chữ nhật đó là x ( cm , x > 5 )
=> Chiều rộng hình chữ nhật đó là x - 5 ( cm )
Theo đề bài ta có : x( x - 5 ) = 300
<=> x2 - 5x - 300 = 0
<=> x2 + 15x - 20x - 300 = 0
<=> x( x + 15 ) - 20( x + 15 ) = 0
<=> ( x + 15 )( x - 20 ) = 0
<=> x = -15 ( không tmđk ) hoặc x = 20 ( tmđk )
=> Chiều dài hình chữ nhật là 20cm
Chiều rộng hình chữ nhật là 20 - 5 = 15cm
Chu vi hình chữ nhật đó là : 2( 20 + 15 ) = 70cm
2/ Gọi độ dài cạnh góc vuông lớn là x( cm , x > 1 )
=> Độ dài cạnh góc vuông nhỏ là x - 1
Theo định lý Pytago ta có :
x2 + ( x - 1 )2 = 52
<=> x2 + x2 - 2x + 1 = 25
<=> 2x2 - 2x + 1 - 25 = 0
<=> 2x2 - 2x - 24 = 0
<=> 2( x2 - x - 12 ) = 0
<=> x2 - x - 12 = 0
<=> x2 + 3x - 4x - 12 = 0
<=> x( x + 3 ) - 4( x + 3 ) = 0
<=> ( x - 4 )( x + 3 ) = 0
<=> x = 4 ( tmđk ) hoặc x = -3 ( không tmđk )
=> Độ dài cạnh góc vuông lớn là 4cm
=> Độ dài cạnh góc vuông bé là 4 - 1 = 3cm
Chu vi hình tam giác = 3 + 4 + 5 = 12cm
1) Gọi chiều dài của hình chữ nhật là \(a\left(a>0,cm\right)\)
Chiều rộng của hình chữ nhật là : \(a-5\left(cm\right)\)
Thoe bài ta có : \(a.\left(a-5\right)=300\Leftrightarrow\left(a-20\right)\left(a+15\right)=0\)
\(\Leftrightarrow a=20\left(a>0\right)\)( Thỏa mãn )
Chiều rộng hình chữ nhật là : \(a-5=15\left(cm\right)\)
Vậy chu vi HCN đó là : \(\left(20+15\right)\cdot2=70\left(cm\right)\)
2) Gọi cạnh góc vuông lớn hơn là \(x\left(x>0,cm\right)\)
Cạnh góc vuông nhỏ hơn là : \(x-1\left(cm\right)\)
Theod dịnh lý Pytago thì : \(x^2+\left(x-1\right)^2=5^2\)
\(\Leftrightarrow2x^2-2x-24=0\)
\(\Leftrightarrow x^2-x-12=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=4\left(x>0\right)\) ( Thỏa mãn )
Vậy cạnh góc vuông còn lại là \(x-1=3\left(cm\right)\)
Chu vi tam giác đó là : \(3+4+5=12\left(cm\right)\)
giả sử tam giác vuông đó là ABC vuông tại A ;cạnh AC >AB
Xét \(\Delta ABC\) vuông tại A có:
BC2=AB2+AC2(Theo định lí Py-ta-go)
\(\Rightarrow5^2=\)AB2+AC2
Mặt khác : AC-AB =1 (cm)\(\Rightarrow\)AC =AB+1
Nên :
\(\Rightarrow25\)= AB2+(AB+1)2
\(\Rightarrow\)25= AB2 +AB2+2AB+1
\(\Rightarrow\)25=2AB2+2AB+1
\(\Rightarrow\)2AB2+2AB +1-25 =0
\(\Rightarrow\)2AB2+2AB-24=0
\(\Rightarrow\)2 (AB2+AB-12)=0
\(\Rightarrow AB^2+AB-12=0\)
\(\Rightarrow\left(AB^2+4AB\right)-\left(3AB+12\right)=0\)
\(\Rightarrow AB\left(AB+4\right)-3\left(AB+4\right)\)=0
\(\Rightarrow\)(AB+4)(AB-3) =0
\(\Rightarrow\left[{}\begin{matrix}AB+4=0\\AB-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}AB=-4\left(loai\right)\\AB=3\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow AB=3cm\)
\(\Rightarrow AC=AB+1=3+1=4\)