
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c/
$C=\frac{11}{2}(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{91.93})$
$=\frac{11}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+...+\frac{93-91}{91.93}\right)$
$=\frac{11}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+....+\frac{1}{91}-\frac{1}{93}\right)$
$=\frac{11}{2}(1-\frac{1}{93})$
$=\frac{11}{2}.\frac{92}{93}=\frac{506}{93}$
d/
$D=5\left(\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+...+\frac{1}{675}\right)$
$=\frac{5}{2}\left(\frac{2}{3}+\frac{2}{15}+\frac{2}{35}+...+\frac{2}{675}\right)$
$=\frac{5}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+...+\frac{27-25}{25.27}\right)$
$=\frac{5}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{25}-\frac{1}{27}\right)$
$=\frac{5}{2}\left(1-\frac{1}{27}\right)$
$=\frac{5}{2}.\frac{26}{27}=\frac{65}{27}$

m: \(\left(-7x+7\right)\left(2x+100\right)=0\)
=>\(\left[{}\begin{matrix}-7x+7=0\\2x+100=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}-7x=-7\\2x=-100\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-50\end{matrix}\right.\)
n: \(2x\left(x+2023\right)\left(-4x+8\right)=0\)
=>\(2\cdot x\left(x+2023\right)\cdot\left(-4\right)\left(x-2\right)=0\)
=>x(x-2)(x+2023)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x+2023=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2023\end{matrix}\right.\)
o: \(-2024x\left(4x-4\right)\left(-2x+6\right)=0\)
=>\(x\left(4x-4\right)\left(-2x+6\right)=0\)
=>\(x\cdot4\left(x-1\right)\cdot\left(-2\right)\left(x-3\right)=0\)
=>x(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x=0\\x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=3\end{matrix}\right.\)
p: -17-2x=199
=>2x=-17-199=-216
=>x=-216/2=-108
q: -24+2x=100
=>2x=100+24=124
=>\(x=\dfrac{124}{2}=62\)
r: \(119-\left(x+5\right)=-21\)
=>\(x+5=119-\left(-21\right)=119+21=140\)
=>x=140-5=135
s: \(-24+\left(-7+x\right)=45\)
=>\(\left(x-7\right)-24=45\)
=>x-31=45
=>x=45+31=76
t: \(-146-\left(-5+x\right)=-6\)
=>\(x-5=-146-\left(-6\right)=-140\)
=>x=-140+5=-135
u: \(-29+4\left(1-5x\right)=-45\)
=>4(1-5x)=-45+29=-16
=>1-5x=-4
=>5x=1+4=5
=>\(x=\dfrac{5}{5}=1\)
v: \(24-5\left(-3+2x\right)=59\)
=>\(24-5\left(2x-3\right)=59\)
=>5(2x-3)=24-59=-35
=>2x-3=-7
=>2x=-4
=>x=-4/2=-2
-17-2x=199
<=>-2x=216
<=>x=-108
-24+2x=100
<=>2x=124
<=>x=62
-24+(-7+x)=45
<=>-7+x=69
<=>x=76
-146-(-5+x)=-6
<=>-146+5-x=-6
<=>x=-135
-29+4(1-5x)=-45
<=>-29+4+20x=-45
<=>20x=-20
<=>x=-1
24-5(-3+2x)=59
<=>24+15-10x=59
<=>-10x=20
<=>x=-2

Bài 3:
a) \(159-\left(25-x\right)=43\)
\(\Rightarrow25-x=159-43\)
\(\Rightarrow25-x=116\)
\(\Rightarrow x=25-116\)
\(\Rightarrow x=-91\)
b) \(\left(79-x\right)-43=-\left(17-52\right)\)
\(\Rightarrow\left(79-x\right)-43=-\left(-35\right)\)
\(\Rightarrow79-x=35+43\)
\(\Rightarrow79-x=78\)
\(\Rightarrow x=79-78\)
\(\Rightarrow x=1\)
c) \(-\left(-x+13-142\right)+18=55\)
\(\Rightarrow-\left(-x+13-142\right)=55-18\)
\(\Rightarrow x-13+142=37\)
\(\Rightarrow x+129=37\)
\(\Rightarrow x=37-129\)
\(\Rightarrow x=-92\)

o: \(\dfrac{-35}{120}=\dfrac{-35\cdot3}{120\cdot3}=\dfrac{-105}{360}\)
\(\dfrac{19}{-45}=\dfrac{-19}{45}=\dfrac{-19\cdot8}{45\cdot8}=\dfrac{-152}{360}\)
mà -105>-152
nên \(-\dfrac{35}{120}>-\dfrac{19}{45}\)
p: \(\dfrac{-12}{48}=\dfrac{-1}{4}=\dfrac{-13}{52}\)
\(\dfrac{-7}{26}=\dfrac{-7\cdot2}{26\cdot2}=\dfrac{-14}{52}\)
mà -13>-14
nên \(-\dfrac{12}{48}>-\dfrac{7}{26}\)
q: \(\dfrac{-8}{-90}=\dfrac{8}{90}\)
\(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{30}{90}\)
mà 8<30
nên \(\dfrac{-8}{-90}< \dfrac{14}{42}\)
r: \(\dfrac{-34}{68}=\dfrac{-1}{2}=\dfrac{-28}{56}\)
\(\dfrac{28}{-51}=\dfrac{-28}{51}\)
56>51
=>\(\dfrac{28}{56}< \dfrac{28}{51}\)
=>\(-\dfrac{28}{56}>-\dfrac{28}{51}\)
=>\(\dfrac{-34}{68}>\dfrac{28}{-51}\)
t: \(\dfrac{-19}{60}< 0\)
\(0< \dfrac{42}{45}=\dfrac{-42}{-45}\)
Do đó: \(\dfrac{-19}{60}< \dfrac{-42}{-45}\)
v: \(\dfrac{1}{-2024}< 0\)
\(0< \dfrac{-2023}{-45}=\dfrac{2023}{45}\)
Do đó: \(\dfrac{1}{-2024}< \dfrac{-2023}{-45}\)
x: Đặt \(A=\dfrac{2024^{2025}+1}{2024^{2026}+1};B=\dfrac{2024^{2000}+1}{2024^{2001}+1}\)
\(2024A=\dfrac{2024^{2026}+2024}{2024^{2026}+1}=1+\dfrac{2023}{2024^{2026}+1}\)
\(2024B=\dfrac{2024^{2001}+2024}{2024^{2001}+1}=1+\dfrac{2023}{2024^{2001}+1}\)
\(2024^{2026}+1>2024^{2001}+1\)
=>\(\dfrac{2023}{2024^{2026}+1}< \dfrac{2023}{2024^{2001}+1}\)
=>2024A<2024B
=>A<B
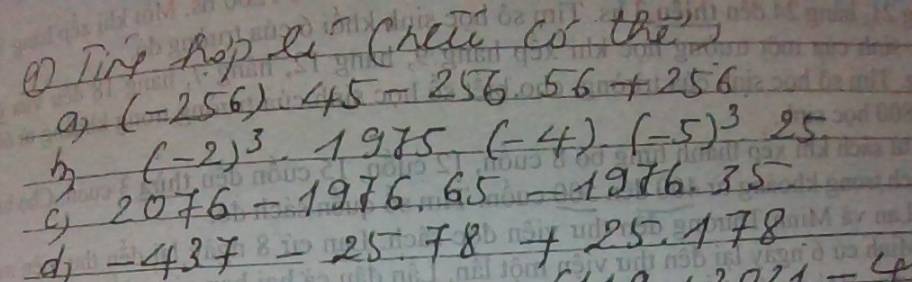 cần giúp gấp vs ạ, em cảm ơn nhìu
cần giúp gấp vs ạ, em cảm ơn nhìu
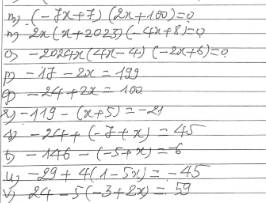
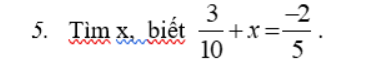 Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!
Giúp mik với ạ mik cần gấp lắm cảm ơn nhìu!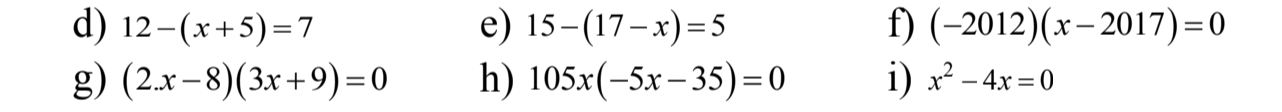


a: \(\left(-256\right)\cdot45-256\cdot56+256\)
\(=256\left(-45-56+1\right)\)
\(=256\left(-100\right)=-25600\)
b: \(\left(-2\right)^3\cdot1975\cdot\left(-4\right)\cdot\left(-5\right)^3\cdot25\)
\(=\left(-8\right)\cdot\left(-125\right)\cdot\left(-4\right)\cdot25\cdot1975\)
\(=1000\cdot\left(-100\right)\cdot1975=-197500000\)
c: \(2076-1976\cdot65-1976\cdot35\)
\(=2076-1976\left(65+35\right)\)
\(=2076-1976\cdot100=2076-197600=-195524\)
d: \(-437-25\cdot78+25\cdot178\)
\(=-437+25\left(178-78\right)\)
\(=-437+2500=2063\)