
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Gọi O là giao của AC và BD
AE//BC nên OE/OB=OA/OC
BF//AD nên OF/OA=OB/OD
mà OA/OC=OB/OD
nen OE/OB=OF/OA
=>EF//AB
b: AB//EF
=>EF/AB=OF/OB=OA/OC=AB/CD
=>AB^2=EF*CD

2
a) \(=x\left(3x^3-x^2+5\right)\)
b) \(=\left(2x+3y\right)\left(x-y\right)\)
c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)
a, = x.(3x3 - x2 + 5)
b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)
c, = x2 - 3x - 4x + 12 = (x2 - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)

Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành

a) \(x^2+2x+1=\left(x+1\right)^2\)
\(x^2-2x+1=\left(x-1\right)^2\)
\(x^2+4x+4=\left(x+2\right)^2\)
\(x^2-4x+4=\left(x-2\right)^2\)
\(x^2+6x+9=\left(x+3\right)^2\)
\(x^2-6x+9=\left(x-3\right)^2\)
\(x^2-10x+25=\left(x-5\right)^2\)
\(x^2+10x+25=\left(x+5\right)^2\)
b) \(16x^2-8x+1=\left(4x-1\right)^2\)
c) \(4x^2+12xy+9y^2=\left(2x+3y\right)^2\)
d) \(x^2+x+\dfrac{1}{4}=\left(x+\dfrac{1}{2}\right)^2\)
e) \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)
f) \(9x^2+30x+25=\left(3x+5\right)^2\)

Bài 3:
a: Ta có: \(3x^2+10x+2=10\)
\(\Leftrightarrow3x^2+10x-8=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\dfrac{2}{3}\end{matrix}\right.\)

a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=x+4\)
=>\(x^2=2x+8\)
=>\(x^2-2x-8=0\)
=>(x-4)(x+2)=0
=>\(\left[{}\begin{matrix}x-4=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
Thay x=4 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot4^2=\dfrac{1}{2}\cdot16=8\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: A(4;8); B(-2;2)
b: Ta có: A(4;8)
=>Tọa độ hình chiếu của A trên trục Ox là:
\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
=>H(4;0)
B(-2;2)
Tọa độ hình chiếu của B trên Ox là:
\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
=>K(-2;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)
Vậy: C(0;4)
H(4;0); K(-2;0)
\(CO=\sqrt{\left(0-0\right)^2+\left(4-0\right)^2}=4\)
\(HK=\sqrt{\left(-2-4\right)^2+\left(0-0\right)^2}=\sqrt{6^2+0}=6\)
Diện tích ΔCHK là:
\(S_{CHK}=\dfrac{1}{2}\cdot CO\cdot HK=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\)

b: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có
CA chung
AB=AE
Do đó: ΔCAB=ΔCAE
Suy ra: \(\widehat{BCA}=\widehat{ECA}\)
hay CA là tia phân giác của \(\widehat{BCE}\)

a) Ta có: \(2x+x^2=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
b) Ta có: \(\left(2x+1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-4\right)\left(2x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)


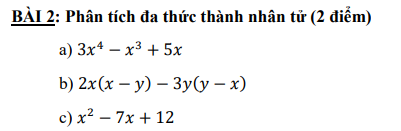
 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
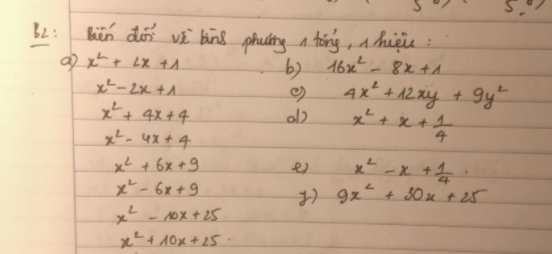



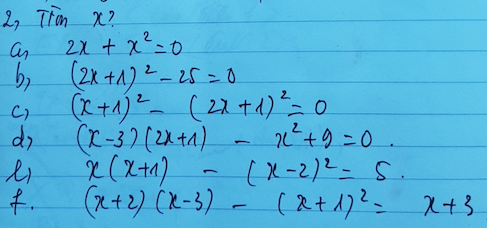
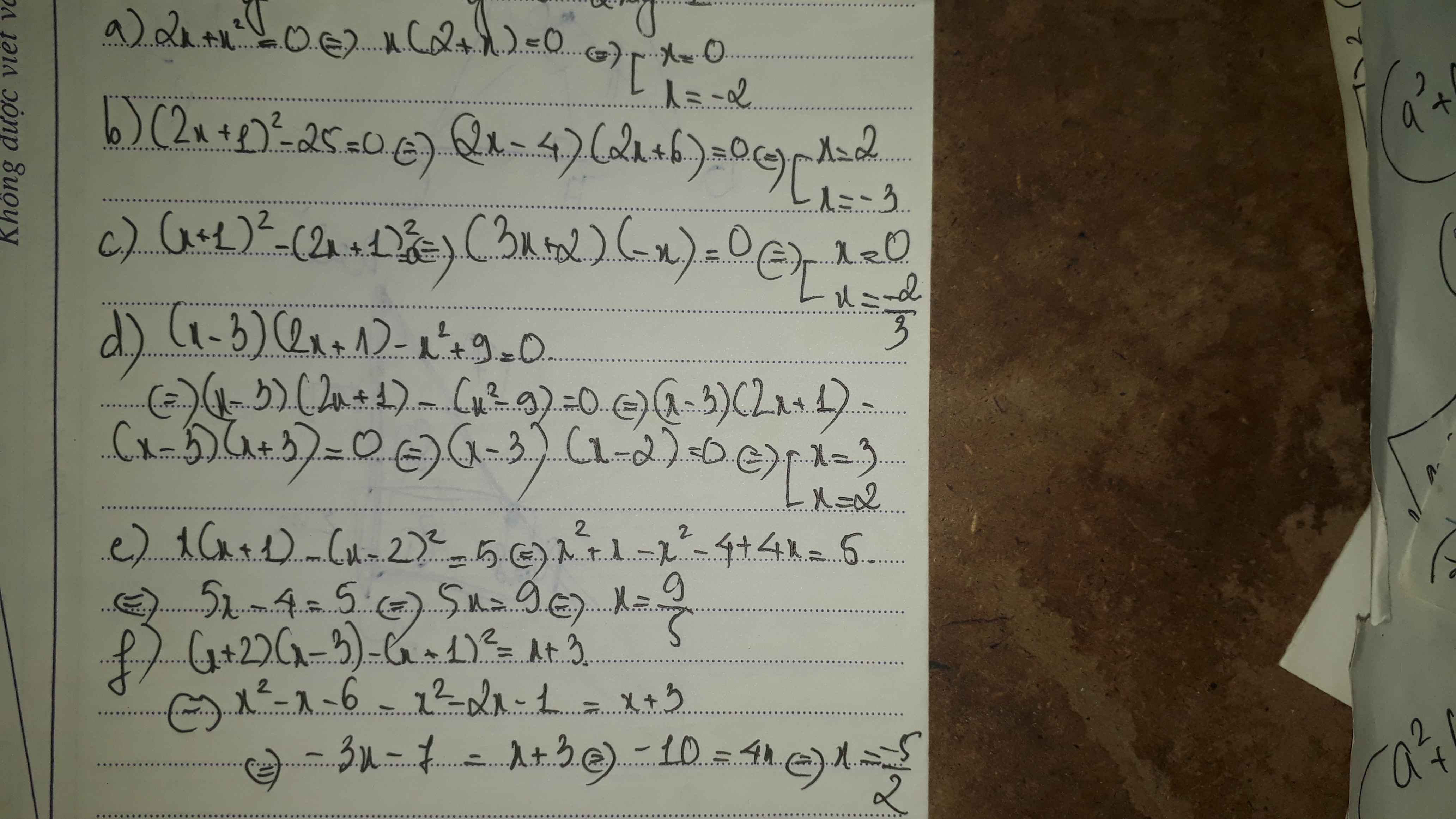
a: Ta có: \(MB=MC=\dfrac{BC}{2}\)
\(NA=ND=\dfrac{AD}{2}\)
\(BA=CD=\dfrac{BC}{2}\)
Do đó: MB=MC=NA=ND=BA=CD
Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
b: Xét tứ giác BMNA có
BM//NA
BM=NA
Do đó: BMNA là hình bình hành
Xét hình bình hành BMNA có BM=BA
nên BMNA là hình thoi
=>BN\(\perp\)AM tại P và P là trung điểm chung của AM và BN
Xét tứ giác CMDN có
CM//DN
CM=DN
Do đó: CMND là hình bình hành
Hình bình hành CMND có CM=CD
nên CMND là hình thoi
=>CN\(\perp\)MD tại Q và Q là trung điểm chung của DM và CN
Xét ΔMAD có
MN là đường trung tuyến
\(MN=\dfrac{AD}{2}\left(=AB\right)\)
Do đó: ΔMAD vuông tại M
Xét tứ giác PMQN có
\(\widehat{PNQ}=\widehat{MPN}=\widehat{MQN}\left(=90^0\right)\)
nên PMQN là hình chữ nhật
c: Để PMQN là hình chữ nhật thì PM=PN
=>AM=BN
Hình thoi ABMN có AM=BN
nên ABMN là hình vuông
=>\(\widehat{ABC}=90^0\)
d: \(AD=2\cdot AB=4\left(cm\right)\)
Xét ΔMAD vuông tại M có \(sinMAD=\dfrac{MD}{AD}\)
=>\(\dfrac{MD}{4}=sin30=\dfrac{1}{2}\)
=>MD=2(cm)
=>MQ=1(cm)
MN=AB
=>MN=2(cm)
ΔMNQ vuông tại Q
=>\(MQ^2+QN^2=MN^2\)
=>\(QN=\sqrt{3}\left(cm\right)\)
Diện tích tứ giác PMQN là:
\(S_{PMQN}=\sqrt{3}\cdot1=\sqrt{3}\left(cm^2\right)\)