Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

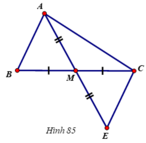
cho tam giác ABC, gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA
a) Chứng minh tam giác ABM = tam giác DCM
b) Chứng minh AB song song với CD
c) Gọi N là trung điểm của AC. Trên tia đối của NB lấy E sao cho NE=NB. Chứng minh D,C,E thẳng hàng
Chúc bạn làm bài tốt
Bài 1: Cho \(\widehat{xOy}\). Lấy A\(\in\)Ox; B\(\in\)Oy sao cho: OA = OB. Vẽ đương tròn tâm A và tâm B có cùng bán kính, sao cho chúng cắt nhau tại hai điểm M và N năm trong \(\widehat{xOy}\).
CMR: a) \(\Delta\)OMA=\(\Delta\)OMB
b) \(\Delta\)ONA=\(\Delta\)ONB
c) Ba điểm O;M;N thẳng hàng
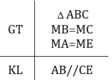
Bài 2: Cho \(\Delta\)ABC có: AB=AC. Gọi M là một điểm năm trong \(\Delta\)ABC, sao cho MB=MC, N là trung điểm của BC.
CMR: a) AM là phân giác của \(\widehat{BAC}\)
b) Ba điểm A;M;N thẳng hàng
Bài 3: Cho\(\Delta\)ABC. M là trung điểm của BC. Trên nửa mặt phẳng bờ là đường thẳng BC không chứa điểm A, vẽ tia Cx // AB. Trên tia Cx lấy điểm D, sao cho CD=AB.
CMR: a) MA=MD
b) Ba điểm A;M;D thẳng hàng

Ba điểm thẳng hàng khi:
+) Ba điểm cùng nằm trên một đường thẳng
+) Có một điểm và chỉ một điểm nằm giữa hai điểm còn lại
Bài tập:
1) Vẽ ba điểm A, B, C thẳng hàng sao cho điểm B nằm giữa hai điểm A và C. Có mấy trường hợp hình vẽ?
2) a) Cho ba điểm A, B, C thẳng hàng thì có mấy trường hợp hình vẽ?
b) Trong mỗi trường hợp, có mấy điểm nằm giữa hai điểm còn lại?
c) Hãy nói cách vẽ ba điểm ko thẳng hàng

Chứng minh thì có rất nhiều kiểu chứng minh: chứng minh 2 tam giác bằng nhau, 2 cạnh bằng nhau, 2 góc bằng nhau hoặc 3 điểm thẳng hàng...Nếu muốn học toán hình giỏi thì phải luyện tập, làm nhiều bài tập. Không chỉ nhờ kiến thức của bạn mà còn nhờ vào sự luyện tập chăm chỉ. Nếu muốn giỏi thì bạn chỉ cần làm nhiều bài tập thôi. Nếu bài nào bạn không biết thì bạn hỏi các bạn khác, dựa vào bài đó thì bạn -> sẽ làm đc những bài tương tự thôi. Bạn đừng lo, nếu có gì không hiểu, bạn có thể hỏi m.n. Các bạn ở đây ai cx thân thiện và tốt bụng hết á...:)

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
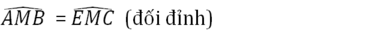
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)



1)xét tam giác MAB và tam giac1 MEC có
BM=CM(M là trung điểm BC)
ME=MA(gt)
góc AMB=góc EMC(đối đỉnh)
nên tam giác MAB = tam giac1 MEC
2)xét tam giác AMC và tam giác EMB có
BM=CM(M là trung điểm BC)
ME=MA(gt)
góc AMC=góc BME(đối đỉnh)
nên tam giác AMC= tam giác EMB
nên góc CAM=góc BEM
mà 2 góc này ở vị trí slt
nên AC//BE
3)ta có tam giác ABM=tam giac1 CEM(cmt)
nên góc BAM=góc CEM
mà 2 góc này ở vị trí slt
nên AB//CE
xét tam giác MBI và tam giac1 MKC có:
BI=CK(gt)
BM=CM(M là trung điểm BC)
góc IBM=góc KCM(slt của AB//CE)
nên tam giác MBI = tam giac1 MKC
nên góc BMI=góc CMK
mà 2 góc này ở vị trí đối đỉnh
nên I,M,K thẳng hàng
Xét ABM và EMC có : AM = ME BM = CM Góc AMB = góc CME ( đối đỉnh ) => tam giac ABM = Tam giác EMC Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong => AB // CE c Xét tam giác AIB và tam gics CIK có : AI = IC BI = Ik Góc AIB = góc CIK ( đối đỉnh ) => tam giác AIB = tam giác CIK
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác .
8. Sử dụng tính chất hình bình hành.
9. Sử dụng tính chất góc nội tiếp đường tròn.
10. Sử dụng góc bằng nhau đối đỉnh
11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng
12. Chứng minh phản chứng
13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0
14. Sử dụng sự đồng qui của các đường thẳng.