K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
0
M
0
26 tháng 7 2018
câu \(31\) này mk giải bằng tay nha . mk không biết cách bấm máy mấy bài bày :(
đặc : \(z=a+bi\) với (\(a\overset{.}{,}b\in R\) và \(i^2=-1\))
ta có : \(\left|z-1-2i\right|=4\Leftrightarrow\left(a-1\right)^2+\left(b-2\right)^2=16\)
\(\Leftrightarrow a^2+b^2=2a+4b+11\)
ta có : \(\left|z+2+i\right|=\sqrt{\left(a+2\right)^2+\left(b+1\right)^2}=\sqrt{a^2+b^2+4a+2b+5}\)
\(=\sqrt{2a+4b+11+4a+2b+5}=\sqrt{6\left(a-1\right)+6\left(b-2\right)+34}\)
áp dụng Bunhiacopxki ta có :
\(\sqrt{\left(6^2+6^2\right)\left[\left(a-1\right)^2+\left(b-2\right)^2\right]}\ge6\left(a-1\right)+6\left(b-2\right)\ge-\sqrt{\left(6^2+6^2\right)\left[\left(a-1\right)^2+\left(b-2\right)^2\right]}\)
\(\Leftrightarrow\sqrt{\left(6^2+6^2\right)\left(16\right)}\ge6\left(a-1\right)+6\left(b-2\right)\ge-\sqrt{\left(6^2+6^2\right)\left(16\right)}\)
\(\Leftrightarrow24\sqrt{2}\ge6\left(a-1\right)+6\left(b-2\right)\ge-24\sqrt{2}\)\(\Rightarrow\sqrt{24\sqrt{2}+34}\ge\sqrt{6\left(a-1\right)+6\left(b-2\right)+34}\ge\sqrt{-24\sqrt{2}+34}\)
\(\Rightarrow\) min của \(\left|z+2+i\right|\) là \(m=\sqrt{-24\sqrt{2}+34}\) và max của \(\left|z+2+i\right|\) là \(M=\sqrt{24\sqrt{2}+34}\)
\(\Rightarrow M^2+m^2=\left(\sqrt{24\sqrt{2}+34}\right)^2+\left(\sqrt{-24\sqrt{2}+34}\right)^2=64\)
AH
0
HT
20 tháng 5 2021
Mình nghĩ những câu tính một chút là ra ngay như này ko cần bấm máy tính đâu, có khi nó lại tốn t/g hơn ngồi tính đấy :v
\(=\int\left(1-\dfrac{1}{\cos^2x}\right)d\left(\cos x\right)\)
\(u=\cos x\Rightarrow....=\int du-\int\dfrac{du}{u^2}=u+\dfrac{1}{u}=\cos x+\dfrac{1}{\cos x}\)
\(\Rightarrow\int\limits^{\dfrac{\pi}{4}}_0...=\cos\dfrac{\pi}{4}-\cos0+\dfrac{1}{\cos\dfrac{\pi}{4}}-\dfrac{1}{\cos0}=\dfrac{3}{\sqrt{2}}+2.\left(-1\right)\)
\(\Rightarrow a^4-b^4=3^4-1=80\)
29 tháng 1
Độ PH của mẫu 1 là:
\(a=-log\left[H^+\right]=-log\left[8\cdot10^{-7}\right]=-\left(log8-7\right)\)
\(=7-log8=7-log2^3=7-3\cdot log2\)
Độ PH của mẫu 2 là:
\(b=-log\left[2\cdot10^{-9}\right]=-\left(log2-9\right)=9-log2\)
\(a-b=7-3\cdot log2-9+log2=-2log2-2< 0\)
=>a<b
=>Độ PH của mẫu 2 lớn hơn
MX
2
HK
25 tháng 2 2021
:)) không ai lại bấm máy tính cả , tất cả sẽ đơn giản khi giải bằng logarit.
\(333333,33333.10^5=\frac{x}{888888,888888.10^6}\left(x>0\right)\)\(\Leftrightarrow log_e\left(333333,33333.10^5\right)=log_e\left(\frac{x}{888888,888888\cdot10^6}\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333}{100000}.10^5\right)=ln\left(\frac{x}{\frac{111111111111}{125000}\cdot10^6}\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333}{100000}\cdot10^5\right)=ln\left(\frac{125000x}{111111111111.10^6}\right)\)
\(\Leftrightarrow ln\left(33333333333\right)-ln10^5+5ln10=ln\left(\frac{125000x}{111111111111.10^6}\right)\)
\(\Leftrightarrow ln\left(33333333333\right)=ln\left(125000x\right)-ln\left(111111111111.10^6\right)\)
\(\Leftrightarrow ln\left(33333333333.111111111111.10^6\right)=ln\left(125000\right)+ln\left(x\right)\)
\(\Leftrightarrow ln\left(\frac{33333333333.111111111111.10^6}{125000}\right)=lnx\)
\(\Rightarrow x=e^{\left(\frac{33333333333.111111111111.10^6}{125000}\right)}\)hoặc \(x=\frac{33333333333.111111111111.10^6}{125000}\)
HK
25 tháng 2 2021
à nhầm phải là \(x=e^{ln\left(\frac{33333333333.111111111111.10^6}{125000}\right)}\)
PT
1
CM
30 tháng 7 2019
Với t = log 2 x . Ta có phương trình đã cho tương đương với phương trình:
PT
1
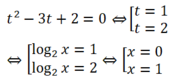
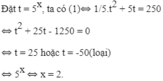
https://hoc24.vn/topic/phuong-phap-giai-tich-phan-3-an-bang-may-tinh-casio.12548
Tham khảo trang đó