K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 11 2016
cái này chắc chỉ có ở sách cũ thôi
Bài 6 / phần luyện tập / trang 109
hình 55
Xét tam giác AHI , ta có :
A + H + HIA = 180
MÀ H = 90 ; A = 40
=> HIA = 180 - 90 - 40 = 50
Vì HIA và KIB là 2 góc đối đỉnh
=> HIA = KIB
Xét tam giác KIB có
K + KIB + B = 180
MÀ K = 90 ; KIB = 50
=> B = 40
20 tháng 11 2016
Hình 56
Gọi giao điểm của EC và BD là I
Xét tam giác DIC , ta có :
D + DIC + ICD = 180
mà ICD = 25 ; CDI = 90
=> DIC = 65
Vì DIC và EIB là 2 góc đối đỉnh
=> DIC = EIB = 65
Xét tam giác EIB , ta có :
IEB + EBI + BIE = 180
=> EBI = 180 - 65 - 90 = 25
TT
0
NH
1
13 tháng 7 2016
Tỉ số \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\) có thể rút gọn thành \(\frac{6}{5}\).Thử lại: \(6\frac{1}{\frac{5}{5\frac{1}{6}}}\)=\(\frac{31}{\frac{5}{\frac{31}{6}}}\)=\(\frac{31}{5}\).\(\frac{6}{31}\)=\(\frac{6}{5}\)
ta có thể viết tỉ số khác cũng có thể "rút gọn" như vậy:VD: \(1\frac{7}{\frac{9}{2\frac{1}{7}}}\)=\(\frac{7}{8}\)
SW
1
SN
15 tháng 10 2021
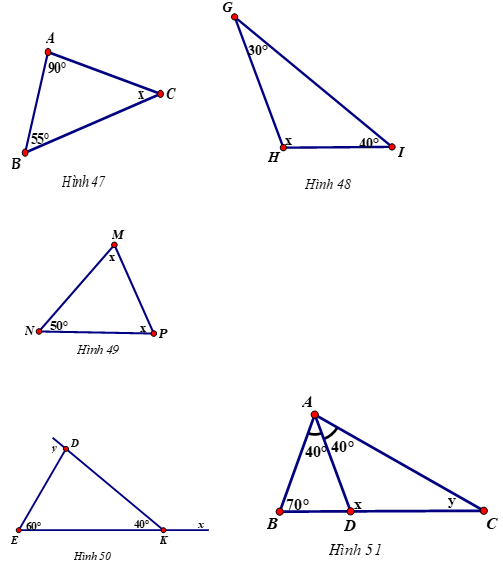
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.
21 tháng 2 2017
Theo định lý Py-ta-go,ta có :
AB2=BC2-AC2
AB2=42-12
AB2=16-1
AB2=15
AB=căn bậc 15
NN
9
14 tháng 10 2021
TL
a) Ta có ˆBIKBIK^ là góc ngoài tại đỉnh II của ΔBAIΔBAI.
Nên ˆBIK=ˆBAI+ˆABI>ˆBAIBIK^=BAI^+ABI^>BAI^
Mà ˆBAK=ˆBAIBAK^=BAI^
Vậy ˆBIK>ˆBAKBIK^>BAK^ (1)
b) Ta có ˆCIKCIK^ là góc ngoài tại đỉnh II của ΔAICΔAIC
nên ˆCIK=ˆCAI+ˆICA>ˆCAICIK^=CAI^+ICA^>CAI^
Hay ˆCIK>ˆCAICIK^>CAI^ (2)
Từ (1) và (2) ta có:
ˆBIK+ˆCIK>ˆBAK+ˆCAIBIK^+CIK^>BAK^+CAI^
⇒ˆBIC>ˆBAC⇒BIC^>BAC^.
Hok tốt nha bn
#Kirito
HN
2
SS
2
MH
15 tháng 11 2021
a) \(\left(x-\dfrac{1}{3}\right)^2=\dfrac{4}{9}\)
⇔ \(\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{2}{3}\\x-\dfrac{1}{3}=-\dfrac{2}{3}\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
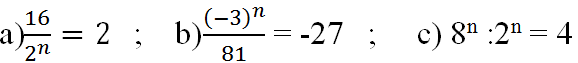
loigiaihay.com
mik ko chắc
a) Theo định nghĩa tập số hữu tỉ là tập hợp các số có thể viết dưới dạng phân số. Hay số hữu tỉ gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
Số vô tỉ là tập hợp gồm các số thập phân vô hạn không tuần hoàn.
Do đó:
Q
∩
I
=
∅
b) Số thực là tập hợp gồm số hữu tỉ và số vô tỉ.
Do đó:
R
∩
I
=
I