K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 12 2023
Sửa đề: a cắt AD,BC lần lượt tại E và F
Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AE}{AD}\left(1\right)\)
Xét ΔBDC có OF//DC
nên \(\dfrac{OF}{DC}=\dfrac{BF}{BC}\left(2\right)\)
Xét hình thang ABCD có EF//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BF}{FC}\)
=>\(\dfrac{ED}{AE}=\dfrac{CF}{BF}\)
=>\(\dfrac{ED+AE}{AE}=\dfrac{CF+BF}{BF}\)
=>\(\dfrac{AD}{AE}=\dfrac{BC}{BF}\)
=>\(\dfrac{AE}{AD}=\dfrac{BF}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra OE=OF
31 tháng 8 2021
Xét tứ giác ABCD có
AB=BC=CD=AD
nên ABCD là hình thoi
Suy ra: \(\widehat{A}=\widehat{C}\)
mà \(\widehat{A}=\widehat{B}\)
nên \(\widehat{B}=\widehat{C}=90^0\)
\(\Leftrightarrow\widehat{A}=\widehat{D}=90^0\)
24 tháng 12 2023
Trên tia Ox, ta có: OM<OP
nên M nằm giữa O và P
=>OM+MP=OP
=>MP=5-2=3cm
Xét ΔOQP có MN//PQ
nên \(\dfrac{OM}{MP}=\dfrac{ON}{NQ}\)
=>\(\dfrac{4}{NQ}=\dfrac{2}{3}\)
=>\(NQ=4\cdot\dfrac{3}{2}=2\cdot3=6\left(cm\right)\)
PH
1
16 tháng 6 2023
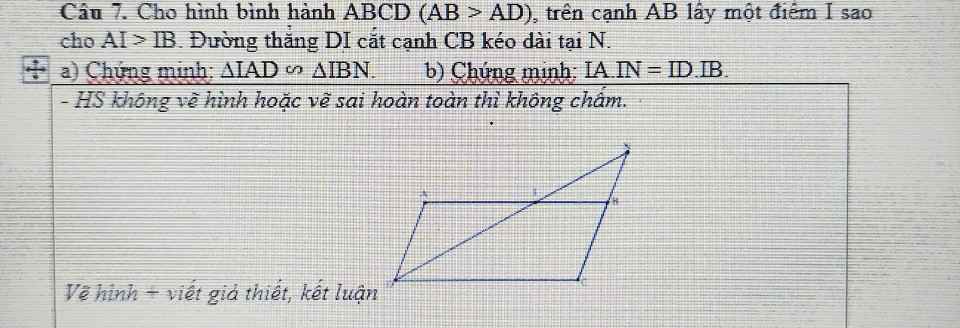
a: Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
b: ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
PH
1
16 tháng 6 2023
Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
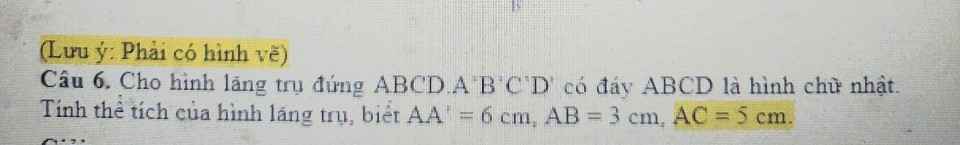
S ABCD=3*4=12cm2
V=12*6=72cm3