Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Ta có : \(\frac{x}{y}=\frac{3}{4}\Rightarrow\frac{x}{3}=\frac{y}{4}\)
Đặt : \(x=3k;y=4k\)
hay \(D=\frac{12k-20k}{9k+16k}=\frac{-8k}{25k}=\frac{-8}{25}\)
Bài 2 :
a, ta có : \(\left|2x-1\right|=\frac{3}{2}\)
TH1 : \(2x-1=\frac{3}{2}\Leftrightarrow2x=\frac{5}{2}\Leftrightarrow x=\frac{5}{4}\)
TH2 : \(2x-1=-\frac{3}{2}\Leftrightarrow2x=-\frac{1}{2}\Leftrightarrow x=-\frac{1}{4}\)
* Với x = 5/4 ta được : \(C=4.\frac{5}{4}+3=8\)
* Với x = -1/4 ta được : \(C=4.\left(-\frac{1}{4}\right)+3=2\)
b, Ta có C = -5/2 hay \(4x+3=-\frac{5}{2}\Leftrightarrow4x=-\frac{11}{2}\Leftrightarrow x=-\frac{11}{8}\)
Vậy với x = -11/8 thì C = -5/2

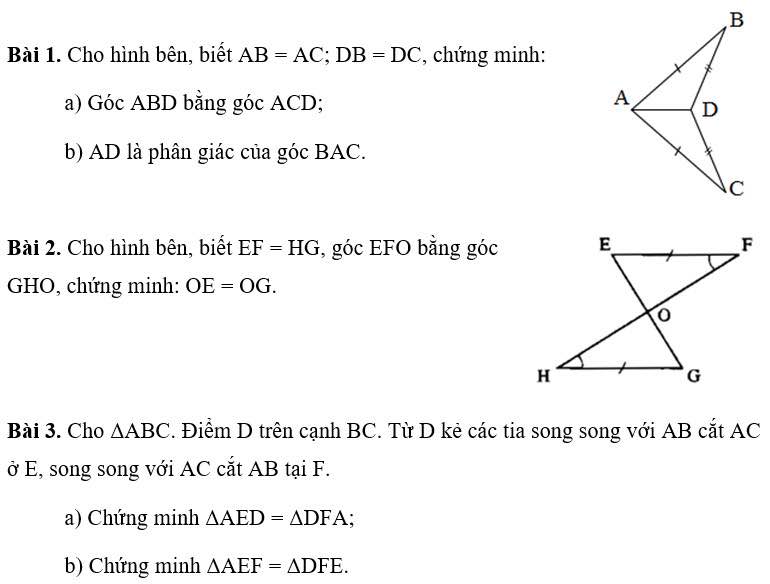
Bài 1 :
a,Có \(AD\) chung , mà \(AB=AC;DB=DC\)
\(\Rightarrow\Delta ABC=\Delta ADC\)
Do đó \(\widehat{ABD}=\widehat{ACD}\)
b,\(AD\) là cạnh chung của 2\(\Delta:\Delta ABD,\Delta ACD\)
\(\Rightarrow AD\) là phân giác của \(\widehat{BAC}\)
Bài 2:
Ta có : \(EF=HG,\widehat{EFO}=\widehat{GHO}\)
Theo TH thứ 2 của 2 tam giác bằng nhau ta có : cạnh - góc - cạnh
\(\Rightarrow OE=OG\)
Bài 3: Có hình ko bn ,mk dựa vào hình lm ko mk lười vẽ hình lắm =(((((((

Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)

\(\frac{5x+7}{4}+\frac{3x+5}{8}>\frac{9x+4}{5}\)
\(\frac{10\cdot\left(5x+7\right)}{40}+\frac{5\cdot\left(3x+5\right)}{40}>\frac{8\cdot\left(9x+4\right)}{40}\)
10.(5x + 7) + 5.(3x + 5) > 8.(9x + 4)
10.(5x + 7) + 5.(3x + 5) - 8.(9x + 4) > 0
50x + 70 + 15x + 25 - 72x - 32 > 0
- 7x + 63 > 0
- 7.(x - 9) > 0
\(\Rightarrow x-9<0\Rightarrow x<9\)

Vì f(x)=ax2+b mà f(0)=3 nên f(0)=a.0+b=3 => f(0)=b=3
Vì f(x)=ax2+b mà f(-2)=-9 nên f(-2)=a.(-2)2+b=-9=>a.4+b=-9 Thay b= 3 ta được :a.4+3=-9=>a.4=-12=>a=-3
Vậy b=3 ;a=-3
nhớ k
 Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi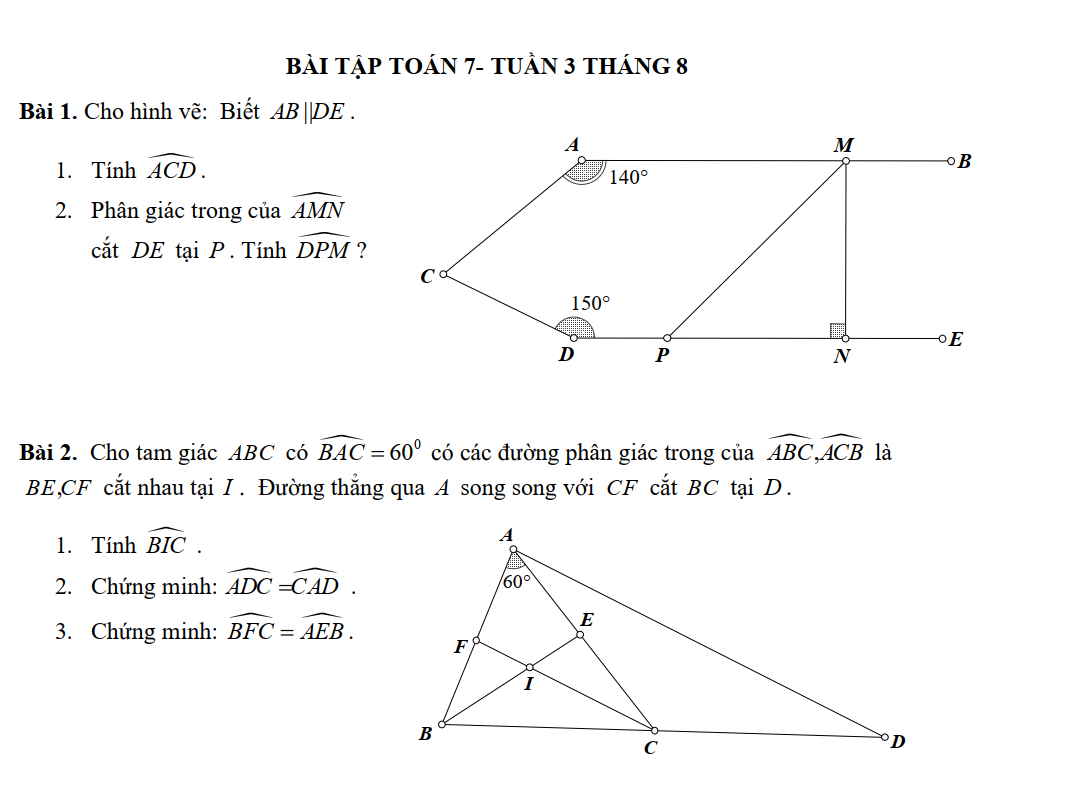

Do \(\overline{2x9y1}\) là số chính phương \(\Rightarrow\overline{2x9y1}=k^2\)
\(\overline{2x9y1}\) có tận cùng bằng 1 \(\Rightarrow k\) tận cùng bằng 1 hoặc 9
Mặt khác \(20164< \overline{2x9y1}< 30276\Rightarrow142^2< \overline{2x9y1}< 174^2\)
\(\Rightarrow142^2< k^2< 174^2\)
\(\Rightarrow142< k< 174\)
Do k có tận cùng bằng 1 hoặc 9 \(\Rightarrow\) k chỉ có thể là 1 trong các số: 149, 151, 159, 161, 169, 171
Kiểm tra ta thấy chỉ có \(k=161\Rightarrow k^2=25921\) là có dạng thỏa mãn \(\overline{2x9y1}\)
Vậy \(\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)