
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3\sqrt{x}-2x=0\)
\(\Leftrightarrow3\sqrt{x}=2x\)
\(\Leftrightarrow\sqrt{x}=\frac{2x}{3}\)
\(\Leftrightarrow\left(\sqrt{x}\right)^2=\frac{4x^2}{9}\)
\(\Leftrightarrow x=\frac{4x^2}{9}\)
\(\Leftrightarrow\frac{4x^2}{x}=9\)
\(\Leftrightarrow4x=9\)
\(\Leftrightarrow x=\frac{9}{4}\)
\(3\sqrt{x}-2x=0\)
\(\Leftrightarrow9x-4x^2=0\)
\(\Leftrightarrow x\left(9-4x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\9-4x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{9}{4}\end{cases}}}\)

6:
1: \(AD\perp AB;BC\perp AB\)
=>AD//BC
2:
AD//BC
=>\(\widehat{C_1}+\widehat{ADC}=180^0\)(trong cùng phía)
=>\(\widehat{C_1}=130^0\)
3:
d là trung trực của AB
=>\(d\perp AB\)
=>d//AD//BC
9:
1: Hai góc so le trong là \(\widehat{xOA};\widehat{BAO}\)
2: BA//Ox
=>\(\widehat{xOA}=\widehat{BAO}\)
mà \(\widehat{xOA}=\widehat{BOA}\)
nên \(\widehat{BAO}=\widehat{BOA}\)
8:
1: BA//Ox
=>\(\widehat{yBA}=\widehat{xOy}\)(hai góc đồng vị)
=>\(\widehat{yBA}=30^0\)
\(\widehat{ABO}+\widehat{yBA}=180^0\)(kề bù)
=>\(\widehat{ABO}=180^0-30^0=150^0\)
2: AC//Oy
=>\(\widehat{xCA}=\widehat{xOy}\)(hai góc đồng vị)
=>\(\widehat{xCA}=30^0\)
\(\widehat{xCA}+\widehat{ACO}=180^0\)(kề bù)
=>\(\widehat{ACO}=180^0-30^0=150^0\)

Ta có : 10^2 = 6^2 + 8^2 ( đúng )
Vậy tam giác có độ dài lần lượt 6dm;8dm;10dm là tam giác vuông
-> chon B

Với x\(\ge1\)\(x-1-\sqrt{x-1}=0< =>x-1=\sqrt{x-1}< =>\left(x-1\right)^2=x-1< =>\left(x-1\right)^2-\left(x-1\right)=0< =>\left(x-1\right)\left(x-1-1\right)=0< =>\left(x-1\right)\left(x-2\right)=0\)\(< =>\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=1\left(TM\right)\\x=2\left(TM\right)\end{matrix}\right.\)


Đặt AB=x; AC=y
Theo đề, ta có: x/3=y/4
Đặt x/3=y/4=k
=>x=3k; y=4k
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2+16k^2=20^2=400\)
=>k=4
=>AB=12cm; AC=16cm

Xét 3 số tự nhiên liên tiếp p, p + 1, p + 2.
Vì p và p + 2 là số nguyên tố lớn hơn 3 => p và p + 2 ko chia hết cho 3 => p + 1 phải chia hết cho 3 (1)
Vì p và p + 2 là số nguyên tố lớn hơn 3 => p và p + 2 ko chia hết cho 2 => p + 1 phải chia hết cho 2 (2)
Từ (1) và (2) kết hợp với ƯCLN (3,2) = 1 => p + 1 chia hết cho 2.3 => p + 1 chia hết cho 6

Bài 3:
b: \(B_1=-\left|2x-3\right|+2\le2\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(B_2=-\left|x+4\right|+5\le5\forall x\)
Dấu '=' xảy ra khi x=-4
Bài 3:
b) Xét số \(-B_3=6+\left|x+4\right|\ge6\Rightarrow B_3\le-6\)
Dấu '=' xảy ra \(\Leftrightarrow x=-4\)


a﴿ Cả 2 vế không âm nên Bình phương 2 vế ta được:
|x + y|2 ≤ ﴾|x| + |y|﴿2
<=> ﴾x+y﴿﴾x+y﴿ ≤ ﴾|x| + |y|﴿. ﴾|x| + |y|﴿
<=> x2 + 2xy + y2 ≤ x2+ 2.|x||y| + y2
<=> xy ≤ |xy| Điều này luôn đúng với mọi x; y
Vậy bất đẳng thức đã cho đúng. Dấu "= " khi |xy| = xy <=> x; y cùng dấu
Với mọi x,y thuộc Q ta luôn có x bé hơn hoặc bằng |y| và -y
=> x+ybes hơn hoặc bằng |x|+|y| và - x-ybes hơn hoặc bằng |x|+|y| hay x+y lớn hơn hoặc bằng -(|x|+|y|)
Do đó -(|x|+|y|) <_ x+y <_ |x|+|y|
Vậy (x+y) lớn hơn hoặc bằng |x|+|y|
 các bạn giúp mk với
các bạn giúp mk với 

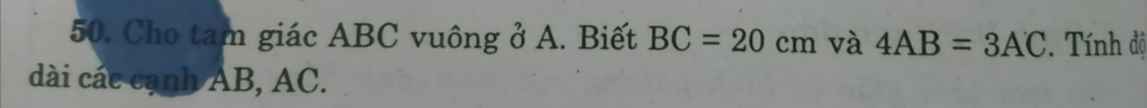
 Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><
Các bạn giúp mk mỗi bài 3 phần b với phần c hoi ạ><