K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Thông cảm mk bị cận!
13 tháng 5 2017
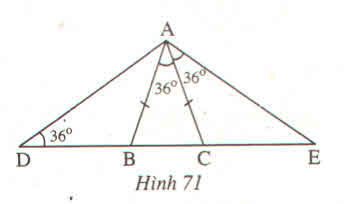
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
SG
1
10 tháng 7 2017
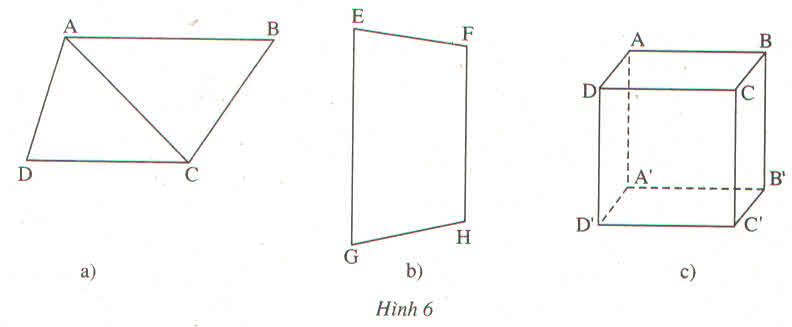
H6a: AB // DC
H6b : EG // FH
H6c: AB // A'B' // D'C' // DC
AD // BC // B'C' // A'D'
AA' // BB' // CC' // DD'
H
20 tháng 4 2017
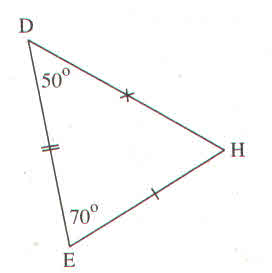
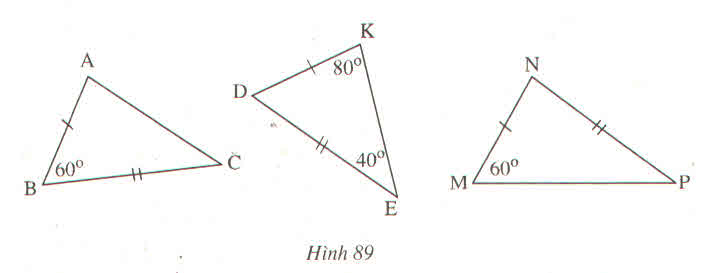
Tam giác DKE có:
\(\widehat{D}+\widehat{K}+\widehat{E}\)=1800 (tổng ba góc trong của tam giác).
\(\widehat{D}\)+800 +400=1800
\(\widehat{D}\)=1800 -1200= \(60^0\)
Nên ∆ ABC và ∆KDE có:
AB=KD(gt)
\(\widehat{B}\)=\(\widehat{D}\)=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại.
