Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
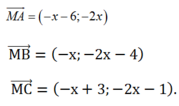
Do đó:
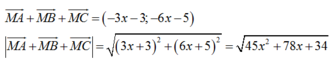
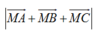
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất
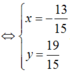

a) Gọi E là trung điểm AB \(\Rightarrow\) \(\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IE}\)
\(\overrightarrow{IA}+\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(2\overrightarrow{IE}+3\overrightarrow{IC}=\overrightarrow{0}\)
b) \(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}+3\overrightarrow{MI}+3\overrightarrow{IC}\right|\)
\(=5MI\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|min\Leftrightarrow MImin\)
\(\Leftrightarrow\) M là hình chiếu của I trên d

Gọi \(M\left(x;y\right)\Rightarrow\left(x+3\right)^2+\left(y+4\right)^2=1\)
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y\right)\\\overrightarrow{MB}=\left(-2-x;1-y\right)\\\overrightarrow{MC}=\left(3-x;4-y\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\left(2-3x;7-3y\right)\)
\(T^2=\left(3x-2\right)^2+\left(3y-7\right)^2\)
Đặt \(\left(x+3;y+4\right)=\left(a;b\right)\Rightarrow a^2+b^2=1\)
\(T^2=\left(3a-11\right)^2+\left(3b-19\right)^2\)
\(T^2=9\left(a^2+b^2\right)-66a-114b+482=491-6\left(11a+19b\right)\)
Ta lại có:
\(\left(11a+19b\right)^2\le\left(11^2+19^2\right)\left(a^2+b^2\right)=482\)
\(\Rightarrow11a+19b\ge-\sqrt{482}\)
\(\Rightarrow T^2\le491+6\sqrt{482}\)
\(\Rightarrow T\le\sqrt{491+6\sqrt{482}}\)
Số liệu bài toán cho xấu 1 cách phi lý và vô nghĩa

\(\overrightarrow{AB}=\left(-6;-3\right)=-3\left(2;1\right)\Rightarrow\) đường thẳng AB nhận \(\left(2;1\right)\) là 1 vtcp
Phương trình tham số đường thẳng AB có dạng: \(\left\{{}\begin{matrix}x=5+2t\\y=4+t\end{matrix}\right.\)
Do M thuộc AB nên tọa độ M có dạng \(M\left(5+2t;4+t\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-2t;-t\right)\\\overrightarrow{MC}=\left(-2-2t;-6-t\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MC}=\left(-2-4t;-6-2t\right)\)
Đặt \(T=\left|\overrightarrow{MA}+\overrightarrow{MC}\right|=\sqrt{\left(-2-4t\right)^2+\left(-6-2t\right)^2}=\sqrt{20\left(t+1\right)^2+20}\ge\sqrt{20}\)
Dấu "=" xảy ra khi \(t+1=0\Rightarrow t=-1\Rightarrow M\left(3;3\right)\)

a) \(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow2\overrightarrow{IA}-\overrightarrow{IA}-\overrightarrow{AB}+\overrightarrow{IA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow2\overrightarrow{AI}=\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow\overrightarrow{AB}+2\overrightarrow{AI}=\overrightarrow{AC}\). Từ đó suy ra cách dựng điểm I:
b) Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
\(\overrightarrow{MN}=2\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}+\overrightarrow{MI}+\overrightarrow{IC}\)
\(=2\overrightarrow{MI}+\left(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}\right)=2\overrightarrow{MI}\)
Suy ra I là trung điểm MN hay MN đi qua điểm I cố định (đpcm).
c) \(\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MB}+\frac{1}{2}\overrightarrow{MN}=\overrightarrow{MA}+\frac{1}{2}\overrightarrow{MC}\)
Đặt K là điểm sao cho \(\overrightarrow{KA}+\frac{1}{2}\overrightarrow{KC}=\overrightarrow{0}\Rightarrow\hept{\begin{cases}K\in\left[AC\right]\\KA=\frac{1}{2}KC\end{cases}}\)tức K xác định
Khi đó \(\overrightarrow{MP}=\overrightarrow{MK}+\overrightarrow{KA}+\frac{1}{2}\overrightarrow{MK}+\frac{1}{2}\overrightarrow{KC}=\frac{3}{2}\overrightarrow{MK}\), suy ra MP đi qua K cố định (đpcm).

MA+MC= MA-MB
<=> 2 MI=BA
=> MI=BA/2
=> I thuộc đường tròn I bán kính AB/2
nãy mk quên giải thik:
a, gọi I la trung điểm của AC=> MA+MC=2MI
hok tốt
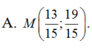
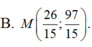
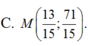
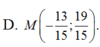
Do M thuộc đường thẳng 2x-y+3=0 nên gọi M(x;2x+3)
gọi G là trọng tâm tam giác ABC
ta có G(-1;4/3)
ta chứng minh được \(3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
=> \(\overrightarrow{3MG}\)=(3.(-1-x);3(4/3-2x-3))
=(-3-x;-5-6x)
=> độ dài \(\overrightarrow{3MG}\)=\(\sqrt{\left(-3-x\right)^2+\left(-5-6x\right)^2}\)=\(\sqrt{37x^2+66x+34}=\sqrt{37\left(x^2+2\frac{33x}{37}+\frac{33^2}{37^2}+\frac{169}{1369}\right)}=\sqrt{37\left(x+\frac{33}{37}\right)^2+\frac{169}{37}}\) vậy GTNN của đọ dài tổng ba véc tơ là \(\frac{13}{\sqrt{37}}\)
đó là đọ dài véc tơ chứ không phải dấu giá trị tuyệt đối đâu nhé
nếu mình sai sót chỗ nào thì bạn cứ theo hướng đó mà làm sẽ ra thôi
thank you bạn