K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
13 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
1 tháng 11 2023
a: \(4x^2-4x\)
\(=4x\cdot x-4x\cdot1\)
\(=4x\left(x-1\right)\)
b: \(x^2-2xy+y^2-4\)
\(=\left(x-y\right)^2-2^2\)
\(=\left(x-y-2\right)\left(x-y+2\right)\)
20 tháng 6 2020
Đặt \(A=\left|x-2018\right|+\left|x-2019\right|+\left|x-2020\right|+\left|x-2021\right|\)
Ta có: \(\hept{\begin{cases}\left|x-2021\right|=\left|2021-x\right|\\\left|x-2020\right|=\left|2020-x\right|\end{cases}}\)
Ta lại có: \(\hept{\begin{cases}\left|x-2018\right|+\left|2021-x\right|\ge\left|x-2018+2021-x\right|=3\\\left|x-2019\right|+\left|2020-x\right|\ge\left|x-2019+2020-x\right|=1\end{cases}}\)
\(\Rightarrow\left|x-2018\right|+\left|x-2019\right|+\left|x-2020\right|+\left|x-2021\right|\ge1+3=4\)
\(\Rightarrow A_{min}=4\)
Dấu '=' xảy ra khi: \(\hept{\begin{cases}\left(x-2018\right).\left(2021-x\right)\ge0\\\left(x-2019\right).\left(2020-x\right)\ge0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2018\le x\le2021\\2019\le x\le2020\end{cases}}\)\(\Rightarrow2018\le x\le2020\)
Vậy \(A_{min}=4\)\(\Leftrightarrow\)\(2018\le x\le2020\)
Nếu các bạn chưa hiểu chỗ suy ra ở chỗ dấu bằng xảy ra thì bạn hãy lập bảng xét dấu nhé ^_^
@#@@# Chúc bn hok tốt #@#@!
5 tháng 12 2021
Bài 4:
\(\left\{{}\begin{matrix}a^4+b^4\ge2a^2b^2\\b^4+c^4\ge2b^2c^2\\c^4+a^4\ge2a^2c^2\end{matrix}\right.\\ \Leftrightarrow2\left(a^4+b^4+c^4\right)\ge2\left(a^2b^2+b^2c^2+c^2a^2\right)\\ \Leftrightarrow a^4+b^4+c^4\ge a^2b^2+b^2c^2+c^2a^2\left(1\right)\\ \left\{{}\begin{matrix}a^2b^2+b^2c^2\ge2ab^2c\\b^2c^2+c^2a^2\ge2abc^2\\c^2a^2+a^2b^2\ge2a^2bc\end{matrix}\right.\\ \Leftrightarrow2\left(a^2b^2+b^2c^2+c^2a^2\right)\ge2\left(a^2bc+ab^2c+abc^2\right)\\ \Leftrightarrow a^2b^2+b^2c^2+c^2a^2\ge a^2bc+ab^2c+abc^2=abc\left(a+b+c\right)\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
1 tháng 11 2023
a: \(9x^3y^2+3x^2y^2\)
\(=3x^2y^2\cdot3x+3x^2y^2\cdot1\)
\(=3x^2y^2\left(3x+1\right)\)
b: \(x^2-2x+1-y^2\)
\(=\left(x^2-2x+1\right)-y^2\)
\(=\left(x-1\right)^2-y^2\)
\(=\left(x-1-y\right)\left(x-1+y\right)\)
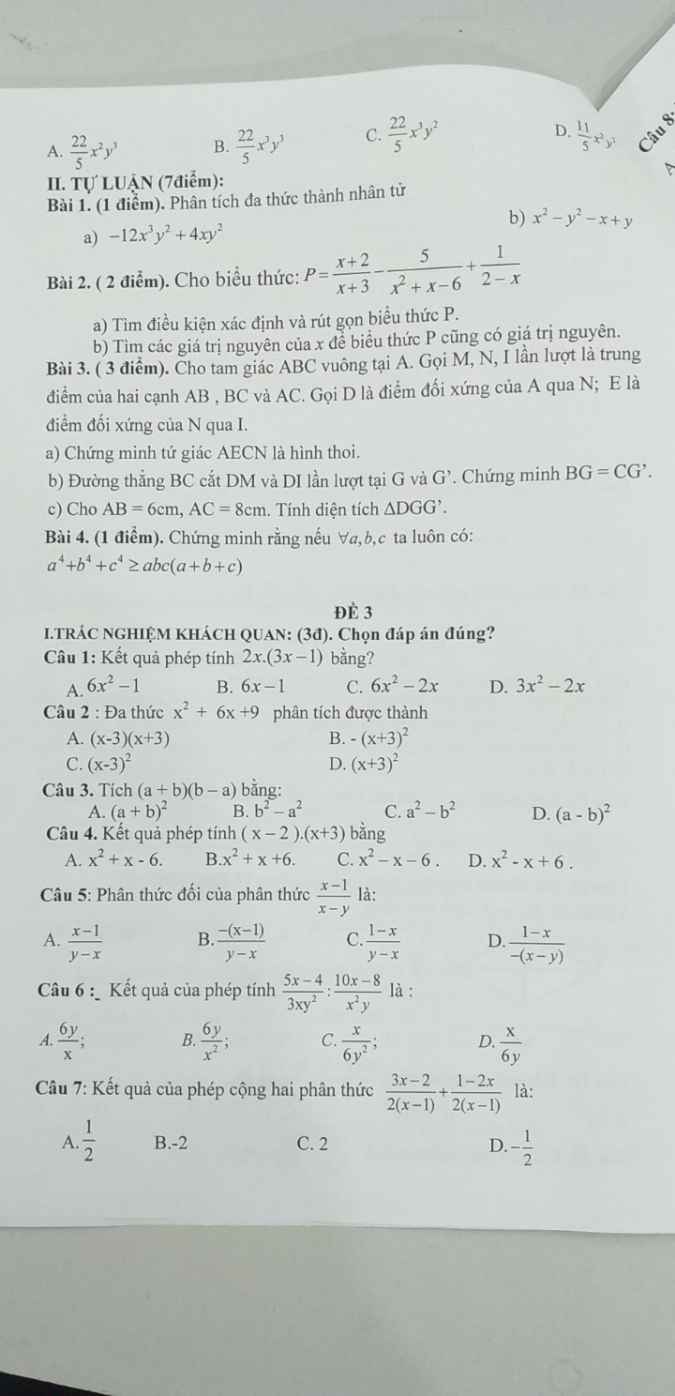
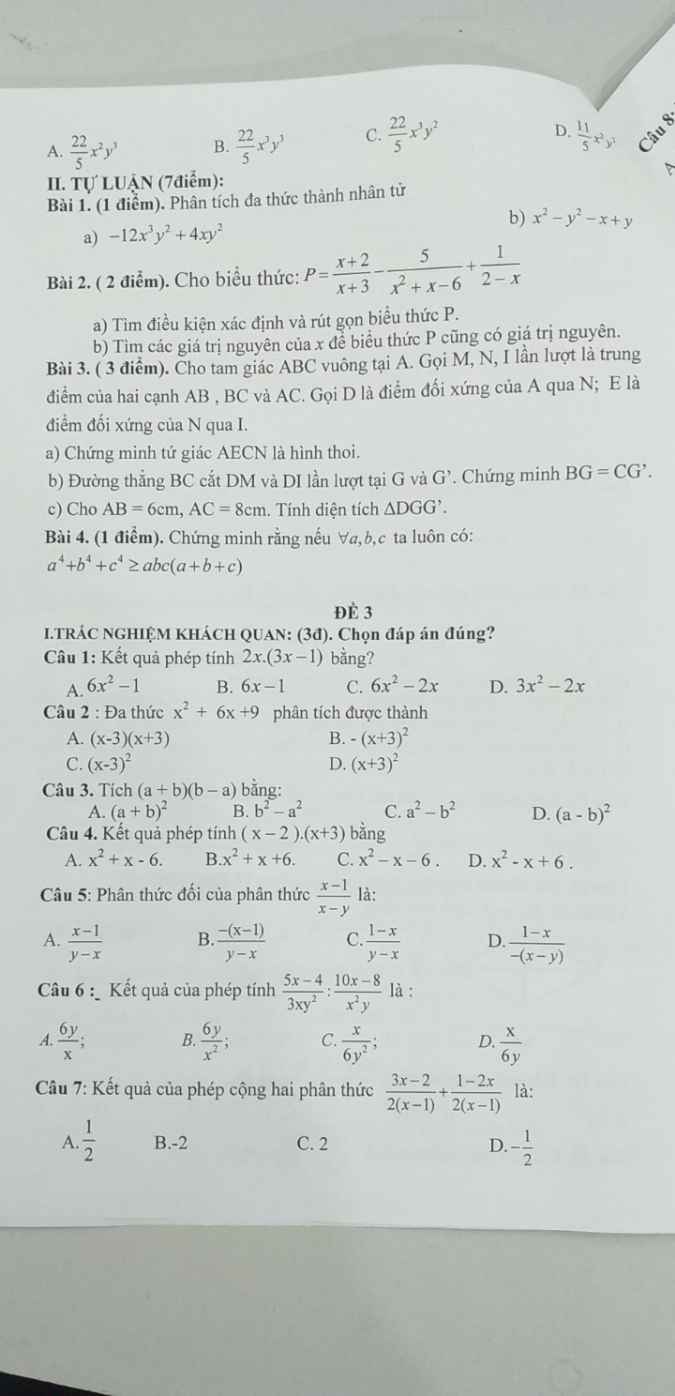
`2x - 3 = 5`
`<=> 2x = 5 + 3`
`<=> 2x = 8`
`=> x = 4`
Vậy `S = {4}`
_____________________
`3x - 4 = 11`
`<=> 3x = 11 + 4`
`<=> 3x = 15`
`=> x = 5`
Vậy `S = {5}`
______________
`(2x + 1)(x - 3) = 0`
`<=>` $\left[\begin{matrix} 2x + 1 = 0\\ x - 3 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 1/2\\ x = 3\end{matrix}\right.$
Vậy `S = {1/2; -3}`
__________________
`(2x - 3)(x + 2) = 0`
`<=>` $\left[\begin{matrix} 2x - 3 = 0\\ x + 2 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 3/2\\ x = -2\end{matrix}\right.$
Vậy `S = {-2; 3/2}`