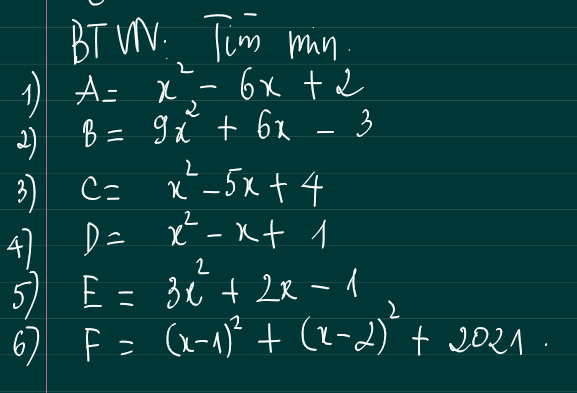Các bạn giúp mình giải bài này nhé !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BK
3 tháng 7 2019
a)999x1001=(1000-1)(1000+1)=10002-12=1000000-1=999999
b)bạn viết đúng đề câu b k thế?
8 tháng 11 2021
4: \(D=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
8 tháng 11 2021
\(A=\left(x^2-6x+9\right)-7=\left(x-3\right)^2-7\ge7\\ A_{min}=7\Leftrightarrow x=3\\ B=\left(9x^2+6x+1\right)-4=\left(3x+1\right)^2-4\ge-4\\ B_{min}=-4\Leftrightarrow x=-\dfrac{1}{3}\\ C=\left(x^2-2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\\ C_{min}=-\dfrac{9}{4}\Leftrightarrow x=\dfrac{5}{2}\\ D=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ D_{min}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(E=3\left(x^2+2\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\\ E_{min}=-\dfrac{4}{3}\Leftrightarrow x=-\dfrac{1}{3}\\ F=x^2-2x+1+x^2-4x+4+2021\\ F=2\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{4031}{2}=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{4031}{2}\ge\dfrac{4031}{2}\\ F_{min}=\dfrac{4031}{2}\Leftrightarrow x=\dfrac{3}{2}\)
S
4 tháng 10 2018
Đặt \(n^2-n+2=a^2\left(a\in N\right)\)
\(\Rightarrow4n^2-4n+8=\left(2a\right)^2\)
\(\Rightarrow\left(2n-1\right)^2+7=\left(2a\right)^2\)
\(\Rightarrow7=\left(2a-2n+1\right)\left(2a+2n-1\right)\)
Vì \(2a+2n-1>2a-2n+1;2a+2n-1>0\) (vì n thuộc N*)
\(\Rightarrow\hept{\begin{cases}2a+2n-1=7\\2a-2n+1=1\end{cases}\Rightarrow4n-2=6\Rightarrow}n=2\)
Vậy n=2 thì ...
20 tháng 11 2023
Bài 2:
1: ĐKXĐ: x<>1
\(\dfrac{x}{x-1}+\dfrac{1}{1-x}\)
\(=\dfrac{x}{x-1}-\dfrac{1}{x-1}\)
\(=\dfrac{x-1}{x-1}=1\)
2: ĐKXĐ: x<>3/2
\(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
=6
3: ĐKXĐ: x<>1/2
\(\dfrac{4x+5}{2x-1}+\dfrac{5-9x}{1-2x}\)
\(=\dfrac{4x+5}{2x-1}+\dfrac{9x-5}{2x-1}\)
\(=\dfrac{4x+5+9x-5}{2x-1}=\dfrac{13x}{2x-1}\)
4: ĐKXĐ: x<>2/5
\(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}=\dfrac{5x-2}{10x-4}=\dfrac{1}{2}\)
5: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{xy}{x^2-y^2}-\dfrac{x^2}{y^2-x^2}\)
\(=\dfrac{xy}{x^2-y^2}+\dfrac{x^2}{x^2-y^2}\)
\(=\dfrac{x\left(x+y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{x}{x-y}\)
6: ĐKXĐ: \(x\notin\left\{0;7\right\}\)
\(\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\)
\(=\dfrac{4x+13}{5x\left(x-7\right)}+\dfrac{x-48}{5x\left(x-7\right)}\)
\(=\dfrac{4x+13+x-48}{5x\left(x-7\right)}\)
\(=\dfrac{5x-35}{x\left(5x-35\right)}=\dfrac{1}{x}\)
7: ĐKXĐ: \(x\ne1\)
\(\dfrac{x+2}{x-1}-\dfrac{x-9}{1-x}-\dfrac{x-9}{1-x}\)
\(=\dfrac{x+2}{x-1}+\dfrac{x-9}{x-1}+\dfrac{x-9}{x-1}\)
\(=\dfrac{x+2+x-9+x-9}{x-1}=\dfrac{3x-16}{x-1}\)
8: ĐKXĐ:x<>1
\(\dfrac{2x^2-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)
\(=\dfrac{2x^2-x}{x-1}-\dfrac{x+1}{x-1}+\dfrac{2-x^2}{x-1}\)
\(=\dfrac{2x^2-x-x-1+2-x^2}{x-1}=\dfrac{x^2-2x+1}{x-1}\)
=x-1
9: ĐKXĐ: x<>3
\(\dfrac{4-x^2}{x-3}+\dfrac{2x-x^2}{3-x}+\dfrac{5-4x}{x-3}\)
\(=\dfrac{4-x^2}{x-3}+\dfrac{x^2-2x}{x-3}+\dfrac{5-4x}{x-3}\)
\(=\dfrac{4-x^2+x^2-2x+5-4x}{x-3}=\dfrac{-6x+9}{x-3}\)
10: ĐKXĐ: x<>5
\(\dfrac{x+1}{x-5}+\dfrac{x-18}{5-x}+\dfrac{x+2}{x-5}\)
\(=\dfrac{x+1}{x-5}-\dfrac{x-18}{x-5}+\dfrac{x+2}{x-5}\)
\(=\dfrac{x+1-x+18+x+2}{x-5}=\dfrac{3x-15}{x-5}=3\)
20 tháng 11 2023
1: \(\dfrac{15x}{7y^3}\cdot\dfrac{2y^2}{x^2}\)
\(=\dfrac{15x\cdot2y^2}{7y^3\cdot x^2}=\dfrac{30xy^2}{7x^2y^3}=\dfrac{30}{7xy}\)
2: \(\dfrac{6x^3}{7y^4}\cdot\dfrac{35y^2}{24x}\)
\(=\dfrac{6x^3}{24x}\cdot\dfrac{35y^2}{7y^4}\)
\(=\dfrac{x^2}{4}\cdot\dfrac{5}{y^2}=\dfrac{5x^2}{4y^2}\)
3: \(\dfrac{4y^2}{x^4}\cdot\dfrac{-3x^2}{8y}\)
\(=\dfrac{4y^2}{8y}\cdot\dfrac{-3x^2}{x^4}=\dfrac{y}{2}\cdot\dfrac{-3}{x^2}=\dfrac{-3y}{2x^2}\)
4: \(\dfrac{-18y^3}{25x^4}:\dfrac{9y^3}{-15x^2}\)
\(=\dfrac{18y^3}{25x^4}\cdot\dfrac{15x^2}{9y^3}\)
\(=\dfrac{18y^3}{9y^3}\cdot\dfrac{15x^2}{25x^4}=2\cdot\dfrac{3}{5x^2}=\dfrac{6}{5x^2}\)
5: \(\dfrac{8y^2}{9x^2}:\dfrac{4y}{3x^2}\)
\(=\dfrac{8y^2}{9x^2}\cdot\dfrac{3x^2}{4y}=\dfrac{8y^2}{4y}\cdot\dfrac{3x^2}{9x^2}=\dfrac{1}{3}\cdot2y=\dfrac{2y}{3}\)
6: \(\dfrac{-20x}{3y^2}:\dfrac{-4x^3}{5y}\)
\(=\dfrac{20x}{3y^2}:\dfrac{4x^3}{5y}\)
\(=\dfrac{20x}{3y^2}\cdot\dfrac{5y}{4x^3}=\dfrac{20x}{4x^3}\cdot\dfrac{5y}{3y^2}=\dfrac{5}{3y}\cdot\dfrac{5}{x^2}=\dfrac{25}{3x^2y}\)
7: \(\dfrac{\left(x+4\right)^2}{4x+12}:\dfrac{x+4}{3x+9}\)
\(=\dfrac{\left(x+4\right)^2}{4\left(x+3\right)}:\dfrac{x+4}{3\left(x+3\right)}\)
\(=\dfrac{\left(x+4\right)^2}{4\left(x+3\right)}\cdot\dfrac{3\left(x+3\right)}{x+4}=\dfrac{3\left(x+4\right)}{4}\)
8: \(\dfrac{5x+10}{4x-8}\cdot\dfrac{4-2x}{x+2}\)
\(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}\)
\(=\dfrac{5\cdot\left(-2\right)}{4}=-\dfrac{10}{4}=-\dfrac{5}{2}\)
9: \(\dfrac{x^2-36}{2x+10}\cdot\dfrac{3}{6-x}\)
\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)}\cdot\dfrac{-3}{x-6}\)
\(=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\)
10: \(\dfrac{x^2-4}{x^2-x}:\dfrac{x^2+2x}{x-1}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-1\right)}\cdot\dfrac{x-1}{x\left(x+2\right)}\)
\(=\dfrac{\left(x-2\right)}{x^2\left(x+2\right)}\)
8 tháng 7 2019
Vì BD là phân giác của ABC và ADC
Xét ∆ADB ta có :
A + ABD + ADB = 180°
ABD + ADB = 180 - 85 = 95°
Mà 2ABD + 2ADB = 95°
=> ABC + ADC = 95 * 2 = 190°
Mà A + ABC + ADC + C = 360°
=> C = 360 - 85 - 190 = 85°
ND
Nguyễn Đức Trí
VIP
20 tháng 8 2023
\(8x^3+12x^2y+6xy^2+y^3-z^3\)
\(=\left(2x+y\right)^3-z^3\)
\(=\left(2x+y-z\right)\left[4x^2+z\left(2x+y\right)+z^2\right]\)
20 tháng 8 2023
a, 8a3 - 36a2 +54ab2 - 27b3
=(8a3-36a2b +54ab2 - 27b3)
=(2a-3b)2
=(2a-3b)(2a-3b)(2a-3b)
b, 8x3 + 12x2y + 6xy2 + y3 - z 3
=(8x3 + 12x2y + 6xy2 + y3) - z3
=(2x + y)3 - y3
=(2x + y +z) . [ (2x + Y)2 + 2(2x + y)+ z2
= (2x + y + z)(4x2 + 4xy + y2 + 4x + 2y + z2