
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 7:
a: Xét ΔABE và ΔMBE có
BA=BM
BE chung
EA=EM
Do đó: ΔABE=ΔMBE


\(Q\left(x\right)-P\left(x\right)=0\)
\(\Leftrightarrow\left(-6x^2+x^3-8+12\right)-\left(x^3-3x^2+6x-8\right)=0\)
\(\Leftrightarrow\left(-6x^2+x^3+4\right)-\left(x^3-3x^2+6x-8\right)=0\)
\(\Leftrightarrow-6x^2+x^3+4-x^3+3x^2-6x+8=0\)
\(\Leftrightarrow-3x^2-6x+12=0\)
\(\Leftrightarrow-3\left(x^2+2x-4\right)=0\)
\(\Leftrightarrow x^2+2x-4=0\)
\(\Leftrightarrow x^2+2x+1=5\)
\(\Leftrightarrow\left(x+1\right)^2=5\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=\sqrt{5}\\x+1=-\sqrt{5}\end{cases}}\Leftrightarrow x=\pm\sqrt{5}-1\)
\(P\left(x\right)-Q\left(x\right)=\left(x^3-3x^2+6x-8\right)-\left(-6x^2+x^3-8+12\right)\)
\(P\left(x\right)-Q\left(x\right)=\left(x^3-3x^2+6x-8\right)-\left(-6x^2+x^3+4\right)\)
\(P\left(x\right)-Q\left(x\right)=x^3-3x^2+6x-8+6x^2-x^3-4\)
\(P\left(x\right)-Q\left(x\right)=3x^2+6x-4\)
Ta cần phân tích \(3x^2+6x-4\) thành nhân tử
Ta có:\(P\left(x\right)-Q\left(x\right)=-\frac{1}{3}\left(-9x^2-18x+12\right)\)
\(=-\frac{1}{3}\left[21-\left(9x^2+18x+9\right)\right]\)
\(=-\frac{1}{3}\left[21-\left(3x+3\right)^2\right]\)
\(=-\frac{1}{3}\left(\sqrt{21}-3x-3\right)\left(\sqrt{21}+3x+3\right)\)
\(\Rightarrow x=\frac{\sqrt{21}-3}{3};x=\frac{-\sqrt{21}-3}{3}\)

Câu 8:
a: Xét ΔAKB và ΔAKC có
AB=AC
BK=CK
AK chung
Do đó: ΔAKB=ΔAKC
b: Ta có: ΔABC cân tại A
mà AK là đường trung tuyến
nên AK là đường cao

Bài 9 :
Thay x = 1 và y = \(\dfrac{1}{2}\) vào biểu thức ; ta có :
\(1^2\left(\dfrac{1}{2}\right)^3+1.\dfrac{1}{2}\)
\(=1.\dfrac{1}{8}+\dfrac{1}{2}\)
\(=\dfrac{1}{8}+\dfrac{1}{2}\)
\(=\dfrac{5}{8}\)

\(\left|x+1\right|và\left|x+2\right|\ge0\)
\(\Rightarrow\orbr{\begin{cases}\left(x+1\right)+\left(x+2\right)=3\\\left(x+1\right)+\left(x+2\right)=-3\end{cases}}\)
\(\orbr{\begin{cases}2x+3=3\\2x+3=-3\end{cases}}\)
\(\orbr{\begin{cases}2x=0\\2x=-6\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
\(\left|x+1\right|+\left|x+2\right|=3\)
Xét \(x+1\ge0;x+2\ge0\Leftrightarrow x\ge-1;x\ge-2\Rightarrow x\ge-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow x+1+x+2=3\Leftrightarrow2x+3=3\Rightarrow x=0\)(TM)
Xét \(x+1\le0;x+2\ge0\Leftrightarrow-2\le x\le-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow-x-1+x+2=3\Leftrightarrow1=3\) (loại)
Xét \(x+1\le0;x+2\le0\Leftrightarrow x\le-1;x\le-2\Leftrightarrow x\le-2\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=-x-2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=-x-1-x-2=-2x-3=3\Rightarrow x=-3\)(TM)
Vậy \(x=\left\{-3;0\right\}\)

\(a,\frac{x+8}{3}+\frac{x+7}{2}=-\frac{x}{5}\)
\(\Leftrightarrow\frac{10\cdot\left(x+8\right)}{30}+\frac{15\left(x+7\right)}{30}=\frac{-6x}{30}\)
\(\rightarrow10x+80+15x+105=-6x\)
\(\Leftrightarrow31x+185=0\)
\(\Leftrightarrow x=-\frac{185}{31}\)
b,\(b,\frac{x-8}{3}+\frac{x-7}{4}=4+\frac{1-x}{5}\)
\(\Leftrightarrow\frac{20\left(x-8\right)}{60}+\frac{15\left(x-7\right)}{60}=\frac{240}{60}+\frac{12\left(1-x\right)}{60}\)
\(\rightarrow20x-160+15x-105=240+12-12x\)
\(\Leftrightarrow47x-517=0\)\(\Leftrightarrow x=11\)



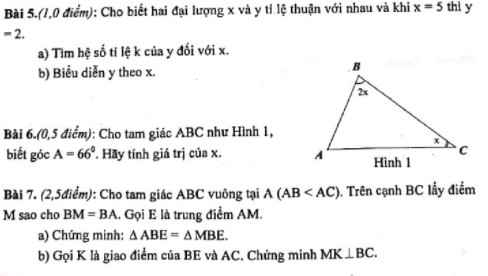
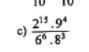 các bạn giúp mik giải đề cương vs nha . mong sự giúp đỡ của các bạn . bài nào bạn biết làm cx đ ko cần làm hết
các bạn giúp mik giải đề cương vs nha . mong sự giúp đỡ của các bạn . bài nào bạn biết làm cx đ ko cần làm hết 


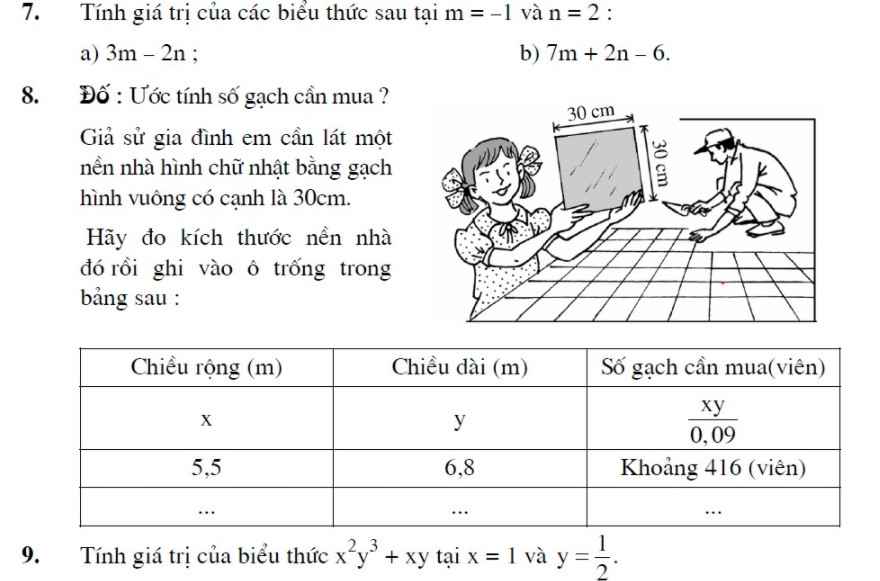 cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik
cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik