Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1000+ 2000= 3000
Mik đầu tiên
Mik chọn quà 1, bạn k cho mik nha

=>1/2.2/3.3/4 = ab.bc.ca
<=> 1/4 = (abc)^2
=> abc = 1/2 hoặc abc = -12
=> a=4/3 ; b = 2/3 ; c=1 hoặc a=-4/3 ; b=-2/3 ; c=-1
k mk nha
Ta có: ab.bc.ac = \(\frac{1}{2}\). \(\frac{2}{3}\).\(\frac{3}{4}\)= \(\frac{1}{4}\)
\(\Leftrightarrow\)(abc)2 =\(\frac{1}{4}\)
\(\Leftrightarrow\)abc = \(\pm\) \(\sqrt{\frac{1}{4}}\)= \(\pm\)\(\frac{1}{2}\)
\(\Rightarrow\)\(\hept{\begin{cases}a=\pm\frac{3}{4}\\b=\pm\frac{2}{3}\\c=\pm1\end{cases}}\)

đáng lẽ kiểm số nhưng t2 khai giảng, t4 hc hình nên cô cho đề dễ lắm, cho hai đt bị 1 đt cắt tạo thành các góc. nêu tên các góc = nhau
đề tùy trg nhé
r`, đây là 2 bài tiêu biểu khó nhất trong = í bài theo như bn t ns c` vs t 2 bài này bt
1) Tìm x;y thuộc N sao cho:
3x.4y = 12x
2) Cho m = 334
a) Tìm tất cả các ước của m. Tính tổng các ước đó
b) Tìm số dư trong phép chia 335 cho 13 (không dùng đồng dư thức)

gọi (d) y=x
Thay x=1=>y=1=> (1;1)
Thay x=2=>y=2=> (2;2)
gọi (d1) y=-2x
Thay x=-1=> y=2=> (-1;2)
Thay x=1=>y=-2=> (1;-2)

3n + 3 + 3n + 1 + 2n + 3 + 2n + 2
= 3n.33 + 3n.3 + 2n.23 + 2n.22
= 3n.(27 + 3) + 2n.(8 + 4)
= 3n.30 + 2n.12
= 3n.5.6 + 2n.2.6
= 6.(3n.5 + 2n.2) \(⋮\) 6

\(a,\frac{13}{x-1}+\frac{5}{2x-2}-\frac{6}{3x-3}=3\)
\(\Leftrightarrow\frac{13}{x-1}+\frac{5}{2\left(x-1\right)}-\frac{6}{3\left(x-1\right)}\)
\(\Leftrightarrow\frac{13.2+5-4}{2\left(x-1\right)}=3\)
\(\Leftrightarrow6\left(x-1\right)=27\)
\(\Leftrightarrow x-1=\frac{9}{2}\Leftrightarrow x=\frac{11}{2}\)
\(b,\frac{2x}{3}-\frac{3}{4}>0\)
\(\Leftrightarrow\frac{8x-9}{12}>0\)
\(\Leftrightarrow8x-9>0\Rightarrow x>\frac{9}{8}\)

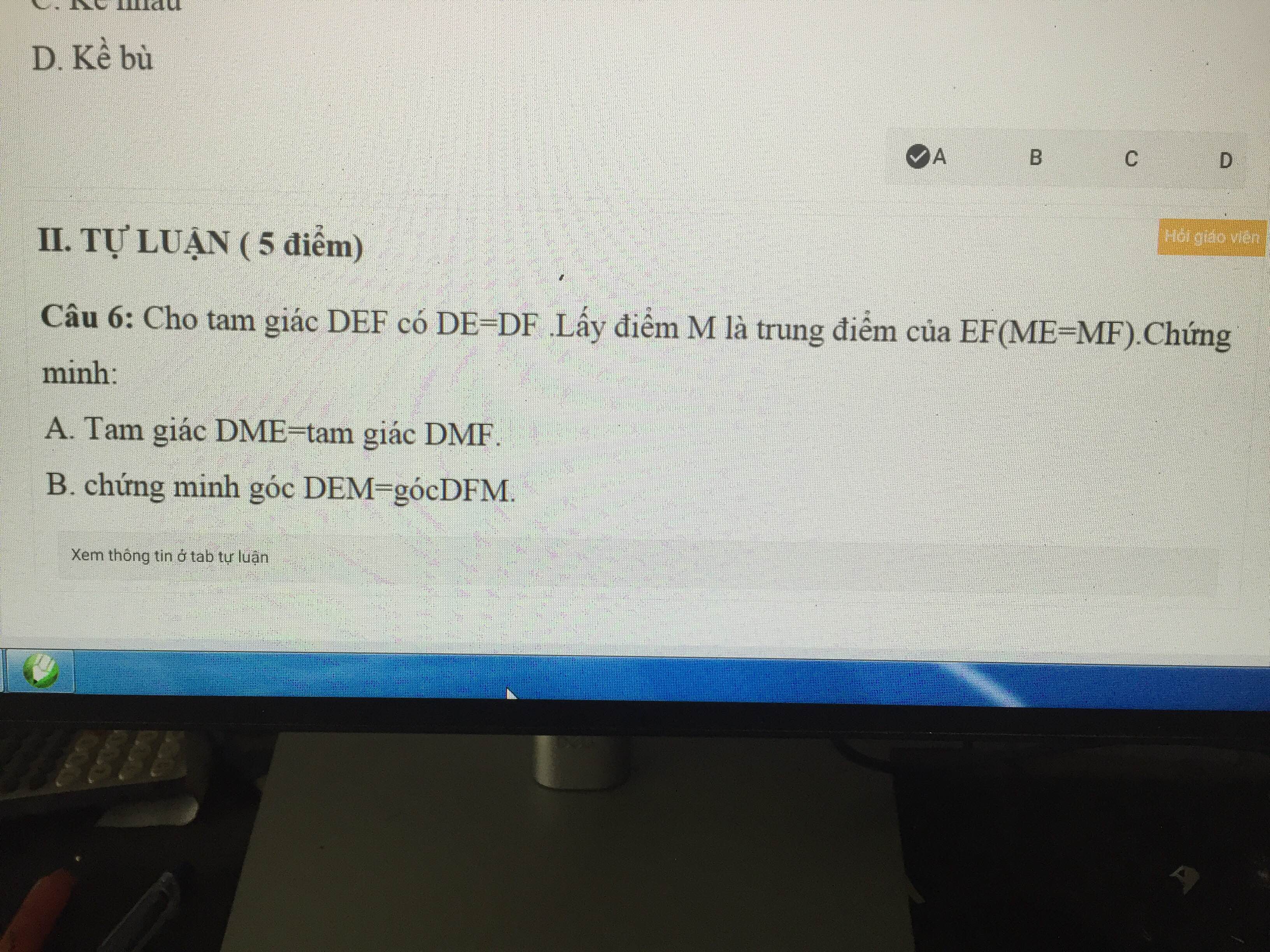
A)Xét tam giác DME và tam giác DMF
Có:DE=DF(gt)
ME=MF(gt)
DM cạnh chung
Do đó:tam giác DME=tam giácDMF

Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
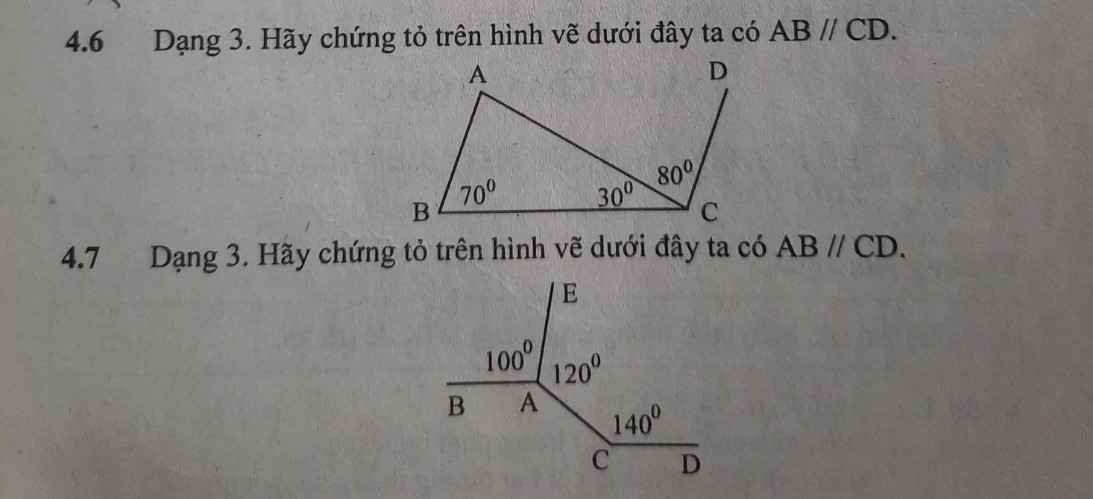

4.6
Ta có: \(\widehat{ABC}+\widehat{DCB}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD