K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
cac ban chia ngang cac hinh ra gium minh nha
8 tháng 2 2019
a, Ta có :tam giác ABD và tam giác ACE có
$\widehat{AEC}=\widehat{ADB}=90$
Góc A chung
=> $\bigtriangleup ABD\sim \bigtriangleup ACE$
b, Tương tự câu a ta CM được $\Delta HEB\sim \Delta HDC (g.g)$
=>$\frac{HE}{HD}= \frac{HB}{HC}\rightarrow HD.HB=HE.HC$
AH
Akai Haruma
Giáo viên
2 tháng 1 2021
Lời giải:
\(|2\overrightarrow{AM}+\frac{1}{2}\overrightarrow{DC}|=|\overrightarrow{AD}+\overrightarrow{DN}|=|\overrightarrow{AN}|=AN\)
Áp dụng định lý Pitago cho tam giác $ADN$ vuông tại $D$ ta có:
\(AN=\sqrt{AD^2+DN^2}=\sqrt{(2a)^2+(\frac{3a}{2})^2}=\frac{5}{2}a\)
Đáp án A
ND
Nguyễn Đức Trí
VIP
31 tháng 8 2023
\(36^{35}.12.234=\left(6^2\right)^{35}.2^2.3.18.13=6^{70}.2^2.3.3^2.2.13=2^{70}.3^{70}.2^3.3^3.13=2^{73}.3^{73}.13\)
25 tháng 4 2019
b)để có giá trị số nguyên thì :
x+3 chia hết x-2
suy ra (x-2)+5 chia hết x-2
mà x-2 chia hết x-2
vậy x thuộc ước của -5
U(-5)=1 ; 5 ; -1 ; -5
HP
4 tháng 4 2021
TH1: \(m=2\)
\(pt\Leftrightarrow-4x+5=0\Leftrightarrow x=\dfrac{5}{4}\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
TH2: \(m\ne2\)
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-\left(m-2\right)\left(m+3\right)>0\\\dfrac{2m}{m-2}>0\\\dfrac{m+3}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6-m>0\\\dfrac{2m}{m-2}>0\\\dfrac{m+3}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -3\\2< m< 6\end{matrix}\right.\)
Vậy \(m\in\left(-\infty;-3\right)\cup\left(2;6\right)\)
HL
3
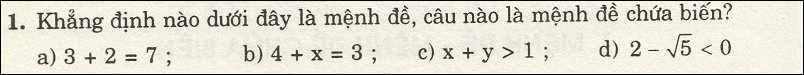
Câu 1 (1,5 điểm):
Đây là phần thống kê rất dễ nên bỏ qua nhé!!!
Câu 2 (3 điểm): Cho hai đa thức:
A(x)=6x2 + 3x4 - 3x + x3 -2
B(x)= -3x4 + 2x - 5x2 + 3 - 6x
a) Tính: A(x) + B(x).
b) Tính: A(x) - B(x).
Câu 3 (1,5 điểm): Thu gọn, tìm bậc rồi tính giá trị của đơn thức sau:
-4(2xy2)2(-3/2x3y) tại x= -1 và y= -1.
Câu 4 (1 điểm): Tìm nghiệm của các đa thức sau:
a) P(x) = -3x + 18
b) Q(x) = -2/3.(1/3 - x) + 5/6
Câu 5 (3 điểm): Cho tam giác ABC cân tại A ( góc A nhọn ). Vẽ hai đường trung tuyến BD, CE của tam giác ABC.
a) Chứng minh: AE=BE=AD=CD
b) Chứng minh: tam giác BCE= tam giác CBD.
c) Chứng minh: DE//BC.
d) Qua điểm M tùy ý trên cạnh BC, vẽ đường thẳng cắt cạnh AC và tia AB lần lượt tại P và Q sao cho M là trung điểm của PQ. Chứng minh: BQ=PC
-Hết-