NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 10 2016
Mình bày cách làm nhé ! Ở 3 câu,mỗi số hạng ở vế trái là trị tuyệt đối nên ko âm
=> Vế trái ko âm và bằng 0 (theo đề) chỉ khi mỗi số hạng bằng 0.Từ đó tìm được x,y
31 tháng 3 2016
Xét tam giác ABD và tam giác ACDcó AB+BD>AD vàAC+CD>AD(BĐT tam giác ABD và ACD)
Cộng 2 vế lại với nhau ta được:
AB+AC+BD+CD>2AD
=>AB+AC+BC>2AD
Mà AB+AC+BC là chu vi của tam giác ABC
=>1/2(AB+AC+BC)>AD
Vậy nửa chu vi của tam giác ABC>AD
15 tháng 2 2019
a) |x - 1,7| = 2,3
Xét 2 trường hợp:
TH1: x - 1,7 = -2,3
x = -2,3 +1,7
x = -0,6
TH2: x - 1,7 = 2,3
x = 2,3 + 1,7
x = 4
Vậy: Tự kl :<
TC
17 tháng 9 2021
em rút gọn 2 tỷ lệ thức của đầu bài cho em sẽ được 9a+2b=a+8b vì đều =7c.
em sẽ tìm được mối liên hệ của a, c với b. rồi khi đó em thay vào tử tính riêng và mẫu tính riêng.
tôi cho em đáp án, nhưng ko giải, em tự làm để rèn luyện kỹ năng nhé.
tử =91/16b\(^2\), mẫu = 116/16b\(^2\)
nên đáp án sẽ là P=91/116 (phân số đã tối giản rồi em nhé)
17 tháng 9 2021
Ta có: \(ac=b^2\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}\)
\(bd=c^2\Rightarrow\dfrac{b}{c}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)\(\Rightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a.b.c}{b.c.d}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\Rightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a^3-b^3+c^3}{b^3-c^3+d^3}=\dfrac{a.b.c}{b.c.d}=\dfrac{a}{d}\left(đpcm\right)\)
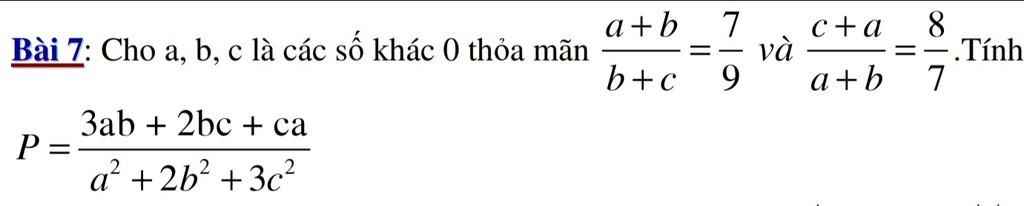
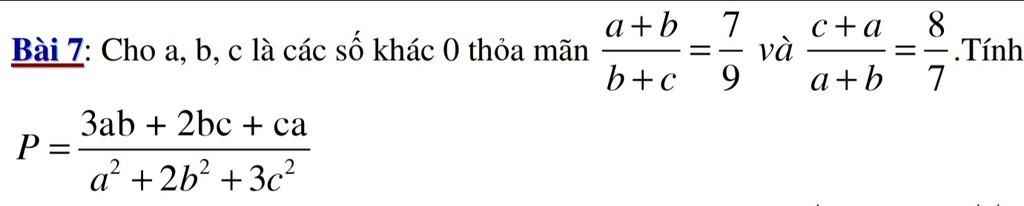
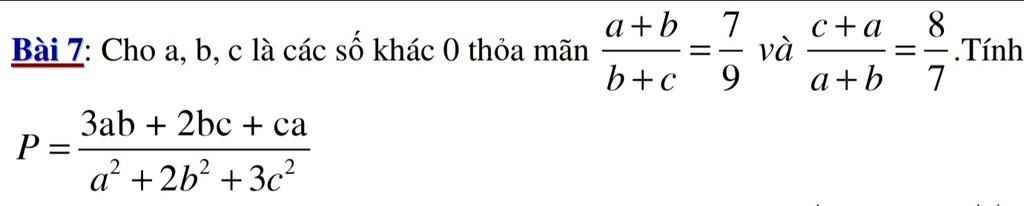
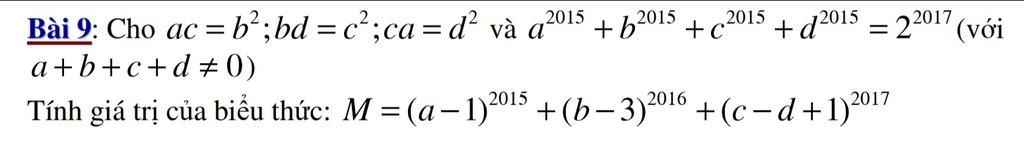
C=(1253.75-1753:5):20192020
C=[(53)3.75-510.75:5)]:20192020
C=[(59.75-510:5.75)]:20192020
C=[(59.75-59.75)]:20192020
C= 0÷20192020
C=0