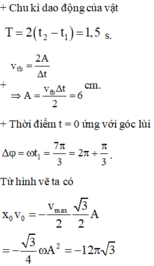Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=2\pi f=\pi; T=\frac{1}{f}=2\left(s\right)\)
\(t=2,5=T+\frac{T}{4}\)
\(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=4\sqrt{2}\left(cm\right)\)
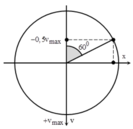
Suy ra, tại t1=0, vật đang ở li độ \(x=\frac{A\sqrt{2}}{2}\) theo chiều âm
Do đó, tại t=t2, vật đã đi được 1 quãng đường là: \(S=4A+A\sqrt{2}=8+16\sqrt{2}\left(cm\right)\)
Tốc độ trung bình là: \(\overline{v}=\frac{S}{t}=\frac{8+16\sqrt{2}}{2,5}\approx12,25\)
Chọn B

Chọn đáp án A
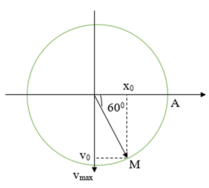
Chu kì dao động của vật:
T = 2 ( t 2 − t 1 ) = 1 , 5 s
v t b = 2 A Δ t ⇒ A = v t b Δ t 2 = 6 c m
Thời điểm t 1 = 1,75s ứng với góc
Δ φ = ω t 1 = 7 π 3 = 2 π + π 3 .
Giả sử thời điêm t 1 vật đang ở biên dương, sử dụng quay ngược lại trước đó 7 π / 3 rad ta xác định được thời điểm t 0 như hình vẽ. Từ đó ta suy ra:
x 0 v 0 = A 2 3 2 v max = 3 4 ω A 2 = 12 π 3

Đáp án C
Hai lần liên tiếp vật có vận tốc bằng 0 ứng với khoảng thời gian là T 2
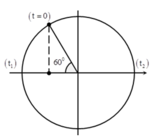
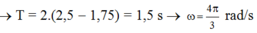
Tốc độ trung bình giữa 2 vị trí trên là:
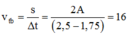
=> A = 6 cm
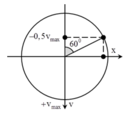
+ Từ t = 0 đến t1 có góc quét là:
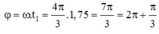
Vậy thời điểm t = 0 có góc lệch là
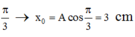
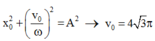
=> ![]()

Đáp án C
+ Ta có: wA = 10π ® A = 5 cm
+ Phương trình của dao động là: x = 5cos(2πt) cm
+ Quỹ đạo dao động là: L = 2A = 10 cm
+ f = ω 2 π Hz => T = 1 s
+ amax = w2A = 20π2 cm/s2
+ vmax = wA = 10π cm/s
+ Trong 1 chu kì thì: v t b = s t = 4 A T = 20 cm/s
+ Khi t = 0 thì vật ở biên dương.
Vậy phát biểu đúng là (c) và (e).