Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta ABH\sim\Delta CAH\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{C_{ABC}}{C_{CAH}}=\dfrac{30}{40}=\dfrac{3}{4}\)
=> \(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}\)
\(\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\\\)
=> \(\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Delta ABH\sim\Delta CBA\)
\(\Rightarrow\dfrac{C_{ABH}}{C_{ABC}}=\dfrac{AB}{BC}\)
=> Chu vi tam giác ABC là 30 . 5 : 3 = 50
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:

Sửa đề: AH=12cm; AB<AC và BC=25cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
hay \(HB\cdot HC=12^2=144\)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên HB+HC=25(cm)
Vì AB<AC nên HB<HC
mà HB+HC=25(cm)
nên \(\left\{{}\begin{matrix}HB< \dfrac{25}{2}=12.5\left(cm\right)\\HC>\dfrac{25}{2}=12.5\left(cm\right)\end{matrix}\right.\)
Ta có: HB+HC=25(cmt)
nên HB=25-HC
Ta có: \(HB\cdot HC=144\)(cmt)
nên \(\left(25-HC\right)\cdot HC=144\)
\(\Leftrightarrow25HC-HC^2-144=0\)
\(\Leftrightarrow HC^2-25HC+144=0\)
\(\Leftrightarrow\left(HC-16\right)\left(HC-9\right)=0\)
\(\Leftrightarrow HC=16\left(cm\right)\)
\(\Leftrightarrow HB=BC-HC=25-16=9\left(cm\right)\)
Vậy: HB=9cm; HC=16cm; \(S_{ABH}=54\left(cm^2\right)\)

Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:



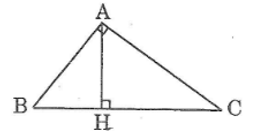

Ta có \(S_{ABC}=S_{ABH}+S_{ACH}=54cm^2+96cm^2=150cm^2\)
Chứng minh tam giác ABH đồng dạng với tam giác ACH \((ABH=ACH\)cùng phụ\()\)
\(\Leftrightarrow\frac{AB^2}{AC^2}=\frac{AH^2}{BH^2}=\frac{S_{BHC}}{S_{AHC}}=\frac{54}{96}=\frac{9}{16}\Leftrightarrow\frac{AH}{BH}=\sqrt{\frac{9}{16}}=\frac{3}{4}=x\Rightarrow\)
\(\Rightarrow AH=4x;HB=3x\)
\(S_{ABH}=\frac{1}{2}AB\cdot BH=54\Rightarrow\frac{1}{2}\cdot4x\cdot3x=54\Rightarrow6x^2=54\Rightarrow x^2=9\Rightarrow x=3\)
\(\Rightarrow HB=3\cdot3=9;AH=4\cdot3=12\)
\(S_{ACH}=\frac{1}{2}AC\cdot CH=96\Rightarrow AC=\frac{96}{6}=16cm\)
\(\Rightarrow BC=HB+HC=9+16=25cm\)
Hình vẽ cho bạn dựa theo :
Chúc bạn học tốt~