Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM

a.
Gọi (D):y=ax+b chứa điểm A, C
(D'):y=a'x+b' chứa điểm B, C
* Ta có: A thuộc (D) khi 1= 2a+b (1)
C thuộc (D) khi 4= 3a+b (2)
Giải hệ (1), (2) ta suy ra a=3 , b=-5
* Ta có: B thuộc (D') khi 3=6a'+b' (3)
C thuộc (D') khi 4=3a'+b' (4)
Giải hệ (3), (4) ta suy ra a=-1/3 , b= 5
Ta thấy: a.a' = 3.(-1/3)=-1
Suy ra (D) vuông góc (D') tại điểm chung C của của 2 cạnh (5)
Vậy tam giác ABC vuông tại C
Theo công thức tính cạnh của đoạn thẳng trong hệ trục tọa độ ta có:
AC=\(\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2}=\sqrt{\left(2-3\right)^2+\left(1-4\right)^2}\)\(=\sqrt{10}\)
BC=\(\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}=\sqrt{\left(6-3\right)^2+\left(3-4\right)^2}\)\(=\sqrt{10}\)
Vậy AC=BC (6)
Từ (5) và (6) ta suy ra tam giác ABC vuông cân tại C
SABC=\(\dfrac{1}{2}\).AB.BC=\(\dfrac{1}{2}.\sqrt{10}.\sqrt{10}=\dfrac{1}{2}.10=\)5 (đvdt)
b. Làm tương tự câu a tìm độ dài các cạnh AB, BD, DA và tính diện tích bằng công thức SABD=\(\sqrt{p\left(p-AB\right)\left(p-BD\right)\left(p-DA\right)}\) với p là nửa chu vi tam giác ABD \(p=\dfrac{1}{2}\left(AB+BD+DA\right)\)
Tiếp tục dùng công thức SABD=\(=\dfrac{1}{2}.AB.BD.sinB\) các số liệu nêu trên đã có, chỉ cần thế vào là có góc B
Gọi I là tâm. Tìm độ dài bán kình bằng công thức SABD=\(\dfrac{AB.BD.DA}{4AI}\)
ta tìm được độ dài AI còn cách xác định tâm thì dựa vào giao điểm 2 đường thẳng (d) chứa đoạn AI và (d') chứa đoạn BI là xong

\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{\left(2x+1\right)^2+\left(x^2-1\right)^2-\left(x^2+x+1\right)^2}{2\left(2x+1\right)\left(x^2-1\right)}\)
\(=\dfrac{-2x^3-x^2+2x+1}{2\left(2x+1\right)\left(x^2-1\right)}=\dfrac{-\left(2x+1\right)\left(x^2-1\right)}{2\left(2x+1\right)\left(x^2-1\right)}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)

\(AB=\sqrt{\left(-2-2\right)^2+\left(-1+2\right)^2}=\sqrt{17}\)
\(AC=\sqrt{\left(1-2\right)^2+\left(2+2\right)^2}=\sqrt{17}\)
Vậy tam giác ABC cân tại A.

Ta có \(S=\dfrac{abc}{4R}=pr=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(\Rightarrow S^2=\dfrac{abcpr}{4R}=p\left(p-a\right)\left(p-b\right)\left(p-c\right)\)
\(\Rightarrow\dfrac{2r}{R}=\dfrac{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}{abc}\)
Theo giả thiết \(\dfrac{a^3+b^3+c^3}{abc}+\dfrac{2r}{R}=4\)
\(\Leftrightarrow\dfrac{a^3+b^3+c^3}{abc}+\dfrac{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}{abc}=4\)
\(\Leftrightarrow a^3+b^3+c^3+\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)=4abc\)
\(\Leftrightarrow a^2b+ab^2+b^2c+bc^2+c^2a+ca^2=6abc\left(1\right)\)
Áp dụng BĐT AM-GM:
\(a^2b+ab^2+b^2c+bc^2+c^2a+ca^2\ge6abc\)
\(\Rightarrow\left(1\right)\) đúng
Đẳng thức xảy ra khi \(a=b=c\)
\(\Leftrightarrow\Delta ABC\) đều

a: vecto AB=(1;3)
vecto AC=(9;-3)
Vì vecto AB*vecto AC=1*9+3*(-3)=0
nên ΔABC vuông tại A
b: ABCD là hình chữ nhật
=>vecto AB=vecto DC
=>10-x=1 và -2-y=3
=>x=9 và y=-5
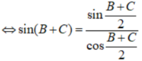
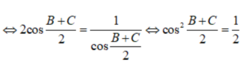
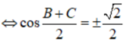
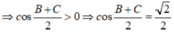
M ở giữa ?
1/ Xét tam giác AMB và tam giác DMC :
AM= D M ( gt)
CM=BM ( gt)
\(\widehat{DMC}=\widehat{AMB}\)
=> \(\Delta AMB=\Delta DMC\)
2/
Từ cặp tam giác trên bằng nhau
=> \(\widehat{ABM}=\widehat{DCM}\)
Mà 2 góc này so le trong
=> \(AB\) // CD
=> \(AC\perp CD\Rightarrow\Delta ACD\) vuông
Xét hai tam giác ABC và CAD , có
CD = AB ( do tam giác AMB = DMC )
AC chung (gt)
góc ACD = góc CAB = 90 độ
=> Tam giác ABC = tam giác CAD ( trường hợp hai cạnh góc vuông )