Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai bài bị trùng nhau nên các bạn nhìn ảnh hay văn bản đều như nhau ạ
c: =>x+2>0
hay x>-2
d: =>-4<=x<=3
e: =>\(x\in\varnothing\)
f: \(\Leftrightarrow\left[{}\begin{matrix}x>4\\x< -6\end{matrix}\right.\)

a) \(x\left(x-6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b) \(\left(-7-x\right)\left(-x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-7-x=0\\-x+5=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-7\\x=-5\end{matrix}\right.\)
c) \(\left(x+3\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+3=0\\x-7=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-3\\x=7\end{matrix}\right.\)
d) \(\left(x-3\right)\left(x^2+12\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\x^2+12=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x^2=-12\text{(vô lý)}\end{matrix}\right.\)
\(\Rightarrow x=3\)
e) \(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x+1\ge0\\2-x\ge0\end{matrix}\right.\\\left[{}\begin{matrix}x+1\le0\\2-x\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\ge-1\\x\le2\end{matrix}\right.\\\left[{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-1\le x\le2\\x\in\varnothing\end{matrix}\right.\)
\(\Rightarrow-1\le x\le2\)
f) \(\left(x-3\right)\left(x-5\right)\le0\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x-3\le0\\x-5\ge0\end{matrix}\right.\\\left[{}\begin{matrix}x-3\ge0\\x-5\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\\\left[{}\begin{matrix}x\ge3\\x\le5\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow3\le x\le5\)
a) =>\(\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b => \(\left[{}\begin{matrix}-7-x=0\\-x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-7\\x=5\end{matrix}\right.\)
d) => \(\left[{}\begin{matrix}x-3=0\\x^2+12=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x^2=-12\end{matrix}\right.\)(vô lí) => x=3

c) \(\left(34-2x\right)\left(2x-6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}34-2x=0\\2x-6-0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=34\\2x=6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=17\\x=3\end{matrix}\right.\)
d) \(\left(2019-x\right)\left(3x-12\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2019-x=0\\3x-12=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2019\\3x=12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2019\\x=4\end{matrix}\right.\)
e) \(57\left(9x-27\right)=0\)
\(\Rightarrow9x-27=0\)
\(\Rightarrow9\left(x-3\right)=0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)
f) \(25+\left(15-x\right)=30\)
\(\Rightarrow25+15-x=30\)
\(\Rightarrow40-x=30\)
\(\Rightarrow x=40-30\)
\(\Rightarrow x=10\)
g) \(43-\left(24-x\right)=20\)
\(\Rightarrow43-24+x=20\)
\(\Rightarrow19+x=20\)
\(\Rightarrow x=20-19\)
\(\Rightarrow x=1\)
h) \(2\left(x-5\right)-17=25\)
\(\Rightarrow2\left(x-5\right)=17+25\)
\(\Rightarrow x-5=21\)
\(\Rightarrow x=21+5\)
\(\Rightarrow x=26\)
i) \(3\left(x+7\right)-15=27\)
\(\Rightarrow3\left(x+7\right)=27+15\)
\(\Rightarrow x+7=14\)
\(\Rightarrow x=14-7\)
\(\Rightarrow x=7\)
j) \(15+4\left(x-2\right)=95\)
\(\Rightarrow4\left(x-2\right)=95-15\)
\(\Rightarrow4\left(x-2\right)=80\)
\(\Rightarrow x-2=20\)
\(\Rightarrow x=20+2\)
\(\Rightarrow x=22\)
k) \(20-\left(x+14\right)=5\)
\(\Rightarrow x+14=20-5\)
\(\Rightarrow x+14=15\)
\(\Rightarrow x=15-14\)
\(\Rightarrow x=1\)
l) \(14+3\left(5-x\right)=27\)
\(\Rightarrow3\left(5-x\right)=27-14\)
\(\Rightarrow3\left(5-x\right)=13\)
\(\Rightarrow5-x=\dfrac{13}{3}\)
\(\Rightarrow x=5-\dfrac{13}{3}\)
\(\Rightarrow x=\dfrac{2}{3}\)

a) \(x+1+x+2+x+3+x+\frac{1}{4}+x+100=7450\)
\(\Leftrightarrow5x+\frac{425}{4}=7540\)
\(\Leftrightarrow x=\frac{5947}{4}\)
Vậy...
b) \(M=3+3^2+3^3+3^4+...+3^{99}+3^{100}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\)
\(=4\left(3+3^3+...+3^{99}\right)⋮4\)
Ta lại có:
\(M=3+3^2+3^3+3^4+...+3^{99}+3^{100}\)
\(=\left(3+3^3\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=\left(3+3^2\right)+3\left(3+3^2\right)+...+3^{98}\left(3+3^2\right)\)
\(=12\left(1+3+...+3^{98}\right)⋮12\)
Chúc bạn học tốt@@
Ai trả lời cho mình sẽ tik cho nhé
(x+1)+(x+2)+(x+3)+...+(x+100)=7450
2x -2^3×3^2=138
(6x-3^4)×7^3=3×74

(x+1)+(x+2)+(x+3)+...+(x+100)=7450
(100x+1+2+3+4+...+100)=7450
100x+5050=7450
100x=7450-5050
100x=2400
x=2400:100
x=24

(x+1)+(x+2)+(x+3)+....+(x+100) = 7450
=> 100x+ (100+1).100:2=7450
<=> 100x+ 5050=7450
<=> 100x= 2400
<=> x=24
Giải:
(x+1)+(x+2)+(x+3)+...+(x+100)=7450
100x+(1+100).100:2 =7450
100x+5050 =7450
100x =7450-5050
100x =2400
x =2400:100
x =24
Chúc bạn học tốt!

a, (x+1)+(x+2)+(x+3)+...+(x+100) = 7450
(x+x+...+x)+(1+2+...+100) = 7450
100 x + 101 . 100 2 = 7450
100x = 2400
x = 24
b, 1+2+3+...+x = 500500
Đặt: A = 1+2+3+...+x
số hạng A (x - 1) : 1 + 1 = x
Tổng của A
A = x + 1 . x 2 = 500500
(x+1).x = 1001000
Ta thấy
1000.1001 = 1001000
=> x = 1000

\(\left(x+1\right)+\left(x+2\right)+...+\left(x+100\right)=7450\)
\(100x+\left(1+2+3+...+100\right)=7450\)
\(100x+\frac{100.101}{2}=7450\)
\(100x+5050=7450\)
\(100x=2400\)
\(\Rightarrow x=24\)
\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+......+\left(x+100\right)=7450\)
\(=>100x+\left(1+2+3+4+5+.....+100\right)=7450\)
\(=>100x+\frac{100.101}{2}=7450\)
\(=>100x=2400\)
\(=>x=24\)
Ủng hộ nha
Thanks
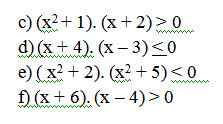 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ
c) (3x-4)(x-1)3=0
\(\Leftrightarrow\orbr{\begin{cases}3x-4=0\\\left(x-1\right)^3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=4\\x-1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{4}{3}\\x=1\end{cases}}}\)
d) (x-4)(x-3)=0
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=3\end{cases}}}\)
e) (x+3)(2-x)>0
=> x+3 và 2-x cung dấu
TH1: Cùng âm
\(\hept{\begin{cases}x+3< 0\\2-x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< -3\\x>2\end{cases}}}\)(loại)
TH2L cùng dương
\(\hept{\begin{cases}x+3>0\\2-x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>-3\\x< 2\end{cases}\Leftrightarrow}-3< x< 2}\)
f) (x+1)+(x+2)+(x+3)+....+(x+100)=7450
<=> (x+x+x+....+x)+(1+2+3++.....+100)=7450
<=> 100x+\(\frac{\left(100+1\right)\cdot100}{2}=7450\)
<=> 100x+5050=7450
<=> 100x=2400
<=> x=24
Toán lớp 6 mà có mấy cái bài này á hả (xàm) -.-