Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng công thức:
Với
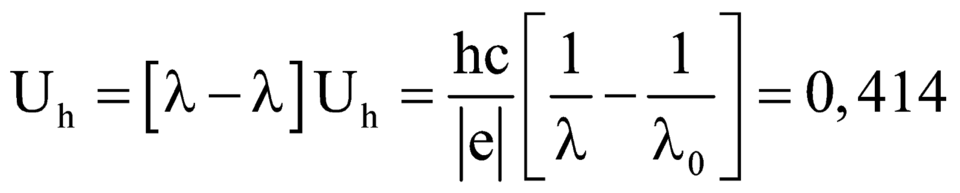(V)
Bán kính lớn nhất trên bề mặt anốt có quang êlectron đập tới là 
mm
Chọn đáp án A.
Chiếu bức xạ λ vào quả cầu kim loại cô lập về điện, thì điện thế cực đại là V, ta có: \(\dfrac{hc}{\lambda}=A_t+W_đ\), với \(W_đ=e.V\)
Chiếu bức xạ λ1: \(\dfrac{hc}{\lambda_1}=A_t+W_{đ1}=2W_{đ1}+W_{đ1}=3W_{đ1}=3.eV_1\)
\(\Rightarrow \dfrac{\lambda_1}{hc}=\dfrac{1}{3eV_1}\) (1)
Với \(A_t=2W_{đ1}=2.eV_1\)
Chiếu bức xạ λ2: \(\dfrac{hc}{\lambda_2}=A_t+W_{đ2}=2.eV_1+5eV_1=7eV_1\)
\(\Rightarrow \dfrac{\lambda_2}{hc}=\dfrac{1}{7eV_1}\) \(\Rightarrow \dfrac{\lambda_1-\lambda}{hc}=\dfrac{1}{7eV_1}\) (2)
Lấy (1) - (2) vế với vế: \(\Rightarrow \dfrac{\lambda}{hc}=\dfrac{4}{21.eV_1}\)
\(\Rightarrow \dfrac{hc}{\lambda}=5,25.eV_1=2eV_1+3,25eV_1=A_t+3,25eV_1\)
Suy ra điện thế cực đại của quả cầu là: \(3,25eV_1\)
Chọn C.
Chọn đáp án C
@ Lời giải:
+ Vận tốc cực đại ban đầu của electron quang điện: v = 2 m e h c λ − A (chú ý đơn vị: tính vận tốc thì A, ε phải đổi đơn vị J)
+ Thay số vào ta được: v = 402721m/s
+ Để các electron vẫn tiếp tục chuyển động thẳng và đều thì cường độ điện trường E → thì lực điện và lực lorenxo phải cân bằng nhau. Khi đó:
qE = qvB → E = vB → B = 201,36 (V/m)
+ Chú ý: Bài này ta không cần quan tâm đến phương, chiều của lực điện và lực lorenxo. Chỉ cần điều kiện cho hai lực này cân bằng nhau là đủ.
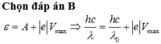
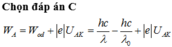
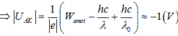
Đáp án B
Khi đã ổn định thì điện thế trên ba tấm kim loại bằng nhau