Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\sqrt{3a}:\sqrt{b}\)
b: \(=\sqrt{a}:\sqrt{xy}\)

a) \(A=\left(1-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+2\right)\)
\(=\left(\dfrac{2}{2}-\dfrac{\sqrt{3}-1}{2}\right):\left(\dfrac{\sqrt{3}-1}{2}+\dfrac{4}{2}\right)\)
\(=\dfrac{2-\left(\sqrt{3}-1\right)}{2}:\dfrac{\left(\sqrt{3}-1\right)+4}{2}\)
\(=\dfrac{3-\sqrt{3}}{2}.\dfrac{2}{\sqrt{3}+3}\)
\(=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}\left(1+\sqrt{3}\right)}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}\)
\(=\dfrac{\left(\sqrt{3}-1\right)^2}{2}\)
Vì \(\left\{{}\begin{matrix}\left(\sqrt{3}-1\right)^2>0\\2>0\end{matrix}\right.\) \(\Rightarrow\dfrac{\left(\sqrt{3}-1\right)^2}{2}>0\) hay A>0
=> A có căn bậc 2
Vậy......
b)\(B=\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right):\dfrac{1}{\sqrt{5}-\sqrt{2}}\)
\(=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)\left(1+\sqrt{3}\right)}{\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}-\sqrt{5}\right):\dfrac{\sqrt{5}+\sqrt{2}}{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)}\)
\(=\left(\dfrac{\sqrt{2}\left(3-1\right)}{1-3}-\sqrt{5}\right).\dfrac{5-2}{\sqrt{5}+\sqrt{2}}\)
\(=\left(-\sqrt{2}-\sqrt{5}\right).\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=-\left(\sqrt{2}+\sqrt{5}\right).\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=-3\)
Vì -3 < 0 hay B < 0
=> B không có căn bậc 2
Vậy.....

\(1,=\left|1-\sqrt{2}\right|+\left|\sqrt{2}+3\right|\\ =1-\sqrt{2}+3+\sqrt{2}\\ =4\\ 2,=\left|\sqrt{3}-2\right|+\left|\sqrt{3}-1\right|\\ =\sqrt{3}-2+\sqrt{3}-1\\ =2\sqrt{3}-3\\ 3,=\left|\sqrt{5}-3\right|+\left|\sqrt{5}-2\right|\\ =\sqrt{5}-3+\sqrt{5}-2\\ =2\sqrt{5}-5\\ 4,=\left|3+\sqrt{2}\right|+\left|3-\sqrt{2}\right|\\ =3+\sqrt{2}+\sqrt{3}-\sqrt{2}\\ =3+\sqrt{3}\\ 5,=\left|2-\sqrt{3}\right|-\left|2+\sqrt{3}\right|\\ =2-\sqrt{3}-\left(2+\sqrt{3}\right)\\ =2-\sqrt{3}-2-\sqrt{3}\\ =-2\sqrt{3}\)

Lời giải:
\(a+b+c=\sqrt{a}+\sqrt{b}+\sqrt{c}=2\)
\(\Rightarrow (\sqrt{a}+\sqrt{b}+\sqrt{c})^2=4\)
\(\Leftrightarrow a+b+c+2(\sqrt{ab}+\sqrt{bc}+\sqrt{ac})=4\)
\(\Leftrightarrow \sqrt{ab}+\sqrt{bc}+\sqrt{ac}=\frac{4-(a+b+c)}{2}=1\)
\(\Rightarrow a+1=a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=(\sqrt{a}+\sqrt{b})(\sqrt{a}+\sqrt{c})\)
Tương tự:
$b+1=(\sqrt{b}+\sqrt{c})(\sqrt{c}+\sqrt{a})$
$c+1=(\sqrt{c}+\sqrt{a})(\sqrt{c}+\sqrt{b})$
Khi đó:
\(A=\left[\frac{\sqrt{a}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}+\sqrt{c})}+\frac{\sqrt{b}}{(\sqrt{b}+\sqrt{a})(\sqrt{b}+\sqrt{c})}+\frac{\sqrt{c}}{(\sqrt{c}+\sqrt{a})(\sqrt{c}+\sqrt{b})}\right]\sqrt{(a+1)(b+1)(c+1)}\)
\(\frac{\sqrt{a}(\sqrt{b}+\sqrt{c})+\sqrt{b}(\sqrt{c}+\sqrt{a})+\sqrt{c}(\sqrt{a}+\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{b}+\sqrt{c})(\sqrt{c}+\sqrt{a})}.\sqrt{(\sqrt{a}+\sqrt{b})^2(\sqrt{b}+\sqrt{c})^2(\sqrt{c}+\sqrt{a})^2}\)
\(=\frac{2(\sqrt{ab}+\sqrt{bc}+\sqrt{ca})}{(\sqrt{a}+\sqrt{b})(\sqrt{b}+\sqrt{c})(\sqrt{c}+\sqrt{a})}.(\sqrt{a}+\sqrt{b})(\sqrt{b}+\sqrt{c})(\sqrt{c}+\sqrt{a})\)
\(=2(\sqrt{ab}+\sqrt{bc}+\sqrt{ac})=2\)

Với \(\begin{cases}a< 0\\b< 0\end{cases}\) thì \(\sqrt{\frac{a}{b}}=\sqrt{-a}:\sqrt{-b}\)
Áp dụng \(\sqrt{\frac{-49}{-81}}=\sqrt{-\left(-49\right)}:\sqrt{-\left(-81\right)}=\sqrt{49}:\sqrt{81}=7:9=\frac{7}{9}\)
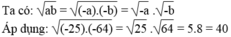
\(\sqrt{ab}=\sqrt{-a}.\sqrt{-b}\) (vì a<0 , b<0)
Áp dụng : \(\sqrt{\left(-25\right).\left(-64\right)}=\sqrt{-\left(-25\right)}.\sqrt{-\left(-64\right)}=\sqrt{25}.\sqrt{64}=5.8=40\)