Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có

Do đó đường thẳng y= 2m- n là TCN
+ Mà y= 0 là tiệm cận ngang của ĐTHS nên 0 = 2m- n
+ Vì x= 0 là TCĐ của ĐTHS nên x= 0 là nghiệm của phương trình x2+ mx+n- 6= 0
Vậy 2 m - n = 0 n = 6 ⇒ m = 3 n = 6 ⇒ m + n = 9
Chọn C.

Chọn B
Phương pháp:
Sử dụng đồ thị hàm số  nhận đường thẳng y =
a
c
làm TCN và đường thẳng x =
-
d
c
làm TCĐ.
nhận đường thẳng y =
a
c
làm TCN và đường thẳng x =
-
d
c
làm TCĐ.
Từ đó tìm được m,n => S
Cách giải:
Đồ thị hàm số y = ( m - 2 n - 3 ) x + 5 x - m - n nhận đường thẳng y = m-2n-3 làm tiệm cận ngang và đường thẳng x = m+n làm tiệm cận đứng.
Từ gt ta có 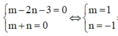
![]()

Đồ thị hàm số y = log a x luôn cắt trục hoành tại điểm (1 ;0), luôn nằm bên phải trục tung (vậy không cắt trục tung), nhận trục tung làm tiệm cận đứng, không có tiệm cận ngang. Vậy chỉ có (I) và (III) đúng
Chọn D

Chọn C.
Với ![]() đồ thị hàm số y =
a
x
+
1
b
x
-
2
nhận đường thẳng x =
2
b
làm tiệm cận đứng
đồ thị hàm số y =
a
x
+
1
b
x
-
2
nhận đường thẳng x =
2
b
làm tiệm cận đứng
Theo đề bài: x = 2 là tiệm cận đứng của đồ thị nên ![]()
Với b ≠ 0 đồ thị hàm số y = a x + 1 b x - 2 nhận đường thẳng y = a b làm tiệm cận ngang.
Theo đề bài: y = 3 là tiệm cận ngang của đò thị hàm số nên ![]()
Vậy a + b = 4.

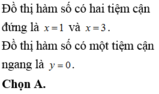



Chọn C.
Ta có:
Nên để đồ thị hàm số nhận trục Ox làm tiệm cận ngang thì n - 3 = 0 ⇔ n = 3
Khi đó hàm số đã cho trở thành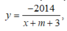
ta có: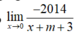 không xác định khi m + 3 = 0
⇔
m = -3
không xác định khi m + 3 = 0
⇔
m = -3
Vậy ta có: m - 2n = -3 - 2.3 = -9