Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
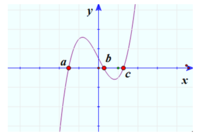
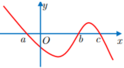
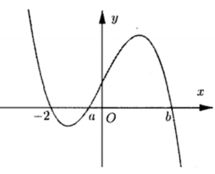
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có

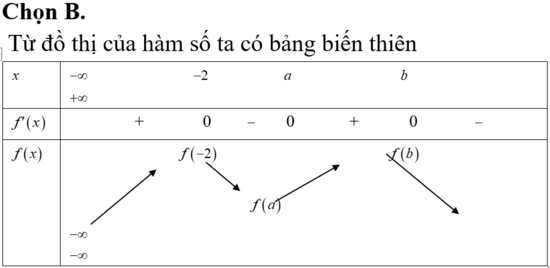
Đáp án B
Giả thiết
![]()
Đặt
![]()
thì
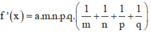
Và
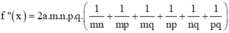
Khi đó, phương trình
![]() (vô nghiệm)
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.

Đáp án là D
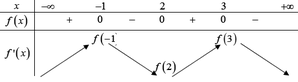
Từ đồ thị f ’(x) ta lập được BBT của f(x)
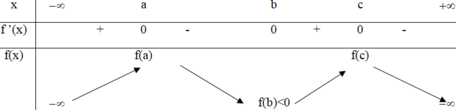
=> Có 4 nghiệm là nhiều nhất

Đáp án D
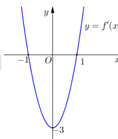
Dựa vào đồ thị hàm số y = f ' ( x ) ⇒ f ' x = 3 x 2 - 1
Khi đó f x = ∫ f ' x d x = x 3 - 3 x + C .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
f x = 4 f x = 0 ⇒ x 3 - 3 x + C = 4 3 x 2 - 1 = 0 ⇔ x = - 1 C = 2 (Do x < 0 suy ra f x = x 3 - 3 x + 2 C
Cho C ∩ O x ⇒ hoành độ các giao điểm là x = -2,x = 1
Khi đó S = ∫ - 2 1 x 3 - 3 x + 2 d x = 27 4 .

Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
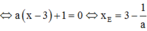
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó 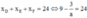
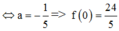


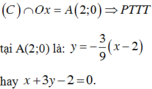
 Tính diện tích S của hình phẳng giới hạn bởi đồ thị
Tính diện tích S của hình phẳng giới hạn bởi đồ thị 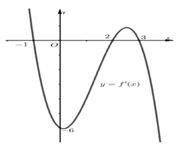



Chọn đáp án B
Ta có f ' x = 4 a x 3 + 3 b x 2 + 2 c x + d
và f ' ' x = 2 6 a x 2 + 3 b x + c
Suy ra g x = f ' x 2 - f ' ' x . f x
Đồ thị hàm số y = f x = a x 4 + b x 3 + c x 2 + d x + e cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 phương trình f x = 0 có 4 nghiệm x 1 , x 2 , x 3 , x 4
Suy ra f x = a x - x 1 x - x 2 x - x 3 x - x 4
*Khi x = x i i = 1 , 2 , 3 , 4 thì
nên g x > 0
*Khi x ≠ x i ∀ i = 1 , 2 , 3 . 4 thì
và f 2 x > 0
Từ (*) suy ra