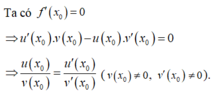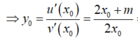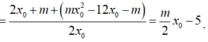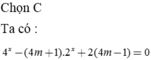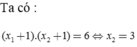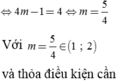Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Xét hàm số 
hàm số liên tục trên R
Có 
đồng biến trên [2;4]
Nên 
Do đó 
Ta có 
Dấu bằng xảy ra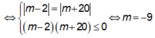 
Vậy 
Chọn D
* Tập xác định 
* Ta có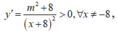 
suy ra hàm số đã cho đồng biến trên đoạn [0;3].
Do đó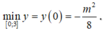 
* Theo yêu cầu bài toán ta có: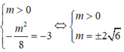 
Chọn D.
Ta có: 
Để hàm số có hai cực trị x1, x2 thì phương trình (1) có hai nghiệm phân biệt.
Khi đó: 
Mà theo yêu cầu bài toán x1, x2 thỏa mãn:
x
1
2
+
x
2
2
=
6
Mặt khác theo Vi-et ta có: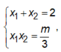 
thay vào (2) ta được 
thỏa mãn điều kiện (*).
Vậy m = -3.
Chọn B
[Phương pháp tự luận]
y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số luôn luôn có cực trị với moi m
Theo định lí Viet
x 1 + x 2 = 2 m x 1 . x 2 = m 2 - 1
x 1 2 + x 2 2 - x 1 x 2 = 7
⇔ ( 2 m ) 2 - 3 ( m 2 - 1 ) = 7
⇔ m = ± 2