Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

Chọn D
* Tập xác định ![]()
* Ta có 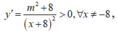
suy ra hàm số đã cho đồng biến trên đoạn [0;3].
Do đó 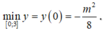
* Theo yêu cầu bài toán ta có: 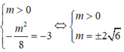
![]()

+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
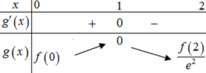
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

Chọn A
ĐK: x ≥ 0
Xét trên 0 ; 3 ta có f ' x = 1 - 1 2 x = 0
⇔ x = 1 4 ∈ 0 ; 3
Ta có:
![]()
Suy ra M = m a x y 0 ; 3 = f 3 = 3 - 3
m = m i n y 0 ; 3 = f 1 4 = - 1 4
Nên M + 2 m ≈ 0 , 768

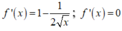
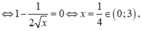
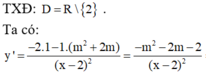
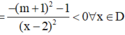
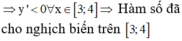
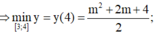
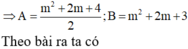

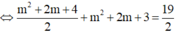
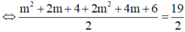



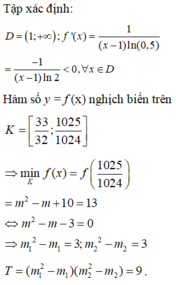
Lời giải:
Có \(f(x)=x-m^2+\frac{m}{x+1}\Rightarrow f'(x)=1-\frac{m}{(x+1)^2}\)
Do $m$ dương nên
\(f'(x)=0\Leftrightarrow (x+1)^2=m\Rightarrow x=\sqrt{m}-1\) hoặc \(x=-\sqrt{m}-1\) (TH này loại vì \(x\geq 0\))
Giờ ta chỉ cần thử giá trị của hàm tại những điểm đặc biệt thôi, vì giá trị cực trị bao giờ cũng xuất hiện ở những điểm đặc biệt của x
\(f(0)=-m^2+m=-2\Leftrightarrow m=2\)
\(f(1)=1-m^2+\frac{m}{2}=-2\Leftrightarrow m=2\)
\(f(\sqrt{m}-1)=\sqrt{m}-1-m^2+\frac{m}{\sqrt{m}-1}=-2\), em shift solve để giải thu được \(m=2,6.....\)
Đến đây theo thông thường ta phải thử lại giá trị của $m$ để tìm đáp án đúng nhất. Nhưng do chỉ tìm giá trị gần nhất thôi nên dễ thấy $m$ gần giá trị $3$ nhât, chọn đáp án B.