Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

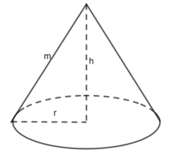
Thể tích hình nón : V = (1/3) π . r 2 h ( c m 3 )
Vậy chọn đáp án B

Gọi H là chin đường cao hạ vuông góc từ đỉnh O đến đường thẳng chắn cung AB
=> H là trung điểm của AB => BH = AH => AB = 2 BH
AD định lý potato vào tam giác OHB vuông tại H ta có
AO2 = OH2+BH2
<=> 132=52 + BH2
=>BH = 12 cm
=> AB = 24 cm

| Bán kính R của đường tròn | 10 | 5 | 3 | 1,5 | 3,2 | 4 |
| Đường kính d của đường tròn | 20 | 10 | 6 | 3 | 6,4 | 8 |
| Độ dài C của đường tròn | 62,8 | 31,4 | 18,84 | 9,42 | 20 | 25,12 |
Kiến thức áp dụng
Đường tròn có bán kính R có :
+ Đường kính : d = 2R.
+ Độ dài đường tròn : C = 2πR.

| Bán kính R của đường tròn | 10 | 5 | 3 | 1,5 | 3,2 | 4 |
| Đường kính d của đường tròn | 20 | 10 | 6 | 3 | 6,4 | 8 |
| Độ dài C của đường tròn | 62,8 | 31,4 | 18,84 | 9,42 | 20 | 25,12 |

Bạn tham khảo bài này nha!
Cho đường tròn (O, R), đường kính AB. Gọi C là điểm chính giữa của cung AB. Vẽ dây cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm DOB. Có mấy đáp số?
Giải

Điểm D có 2 trường hợp :
Nếu điểm D nằm giữa C và B
Ta có C điểm chính giữa của cung AB
số đo cung BC = số đo cung AC = 900
CD = R (gt)
Suy ra : OC = OD = CD = R
⇒ΔOCD⇒ΔOCD đều ⇒ˆCOD=600⇒COD^=600
⇒⇒ sđ cung CD = sđ cung COD = 600
⇒⇒ sđ cung BD = sđ cung BC - sđ cung CB = ${90^0} - {60^0} = {30^0}\)
ˆBODBOD^ = sđ cung BD = 300
Nếu C nằm giữa B và D ta có : CD = OC = OD = R
⇒ΔOCD⇒ΔOCD đều ⇒ˆCOD=600⇒COD^=600
sđ cung CD = sđ cung COD = 600
sđ cung BD = sđ cung BC + sđ cung CD= 900+600=1500900+600=1500
ˆBODBOD^ = sđ cung BD = 1500

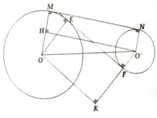
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

Đề không nói rõ là đoạn thẳng OC cắt đường tròn hay đường thẳng OC. Vì nếu là đường thăng thì sẽ có hai điểm D. Ta coi D là giao điểm của đoạn thẳng OC với đường tròn, nếu D là giao của tia đối của tia OC với đường tròn thì chỉ việc cộng thêm 2R.
Tam giác OAB có \(OA=OB=AB=R\to\Delta OAB\) đều. Suy ra \(\angle OBA=60^{\circ}.\) Do \(BC=BA=OB=R\to\Delta BCO\) cân ở B. Vậy theo tính chất góc ngoài tam giác \(\angle OBA=\angle BOC+\angle BCO=2\angle BCO\to\angle BCO=\frac{60^{\circ}}{2}=30^{\circ}.\) Vậy góc ACD bằng 30 độ.
Kẻ OH vuông góc với AB. Vì tam giác OAB đều nên \(OH=\frac{\sqrt{3}}{2}AB=\frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}.\) Tam giác OHC vuông ở H có góc đỉnh C bằng 30 độ nên \(OH=\frac{1}{2}OC\to OC=2\times\frac{3\sqrt{3}}{2}=3\sqrt{3}.\) Mà \(OD=R=3\to CD=OC-OD=3\sqrt{3}-3.\)
Chọn đáp án D
Độ dài cung 60 ° là: