Biến đổi thành tích các biểu thức sau:a. 1 – sinxb. 1 + sinxc. 1 + 2cosxd. 1

Khách

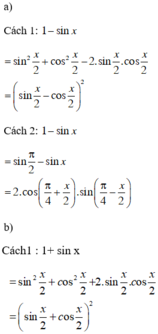
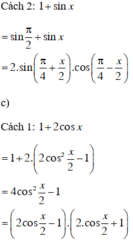
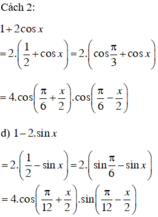
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

1 tháng 7 2017

Biến đổi thành tích các biểu thức sau:

a. 1 – sinx

b. 1 + sinx

c. 1 + 2cosx

d. 1 – 2sinx

#Toán lớp 10

Cao Minh Tâm

1 tháng 7 2017

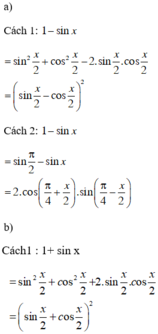
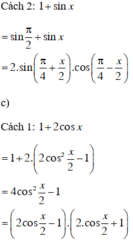
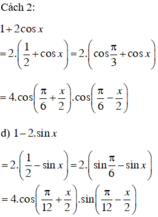
Giải bài 7 trang 155 SGK Đại Số 10 | Giải toán lớp 10

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

28 tháng 8 2018

Biến đổi biểu thức sina + 1 thành tích.

#Toán lớp 10

Cao Minh Tâm

28 tháng 8 2018

Chọn A.

Áp dụng công thức nhân đôi và chú ý: (đây là 2 góc phụ nhau)

Đúng(0)

Kiều Bảo Anh

24 tháng 6 2021

Biến đổi thành tích biểu thức sau:

sin3x+sinx-sin2x+2(1-cosx)cosx

#Toán lớp 10

Nguyễn Việt Lâm

Giáo viên

24 tháng 6 2021

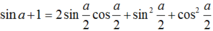
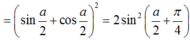
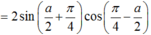
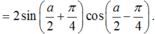
$=2sin2x.cosx-2sinx.cosx+2cosx-2cos^2x$

$=2cosx\left(sin2x+1\right)-2cosx\left(sinx+cosx\right)$

$=2cosx\left(2sinx.cosx+sin^2x+cos^2x\right)-2cosx\left(sinx+cosx\right)$

$=2cosx\left(sinx+cosx\right)^2-2cosx\left(sinx+cosx\right)$

$=2cosx\left(sinx+cosx\right)\left(sinx+cosx-1\right)$

Đúng(3)

Minh châu Hà

19 tháng 5 2021

Biến đổi thành tích các biểu thức sau A= cos2x + sin4x - cos6x B = sinx - sin2x + sin5x + sin8x

#Toán lớp 10

Lê Thị Thục Hiền

19 tháng 5 2021

$A=cos2x+sin4x-cos6x$

$=\left(cos2x-cos6x\right)+sin4x=-2.sin4x.sin\left(-2x\right)+sin4x$

$=2sin4x.sin2x+sin4x=sin4x\left(2sin2x+1\right)$

$B=sinx-sin2x+sin5x+sin8x$

$=\left(sin5x+sinx\right)+\left(sin8x-sin2x\right)$

$=2.sin3x.cos2x+2.sin3x.cos5x$

$=2sin3x\left(cos2x+cos5x\right)$

Đúng(0)

Đặng Hoàng Anh

8 tháng 8 2021 - olm

Biến đổi biểu thức sau thành tích:

a) $1-sin(x)$

b) $1+sin(x)$

c) $1-2cos(x)$

d) $1+2cos(x)$

#Toán lớp 10

Nguyễn Văn Lâm ( ✎﹏IDΣΛ亗 )

13 tháng 8 2021

$a)$

$1-sin\left(x\right)$

$=sin^2\frac{x}{2}+cos^2\frac{x}{2}-2.sin\frac{x}{2}.cos\frac{x}{2}$

$=\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2$

$b)$

$1+sin\left(x\right)$

$=sin^2\frac{x}{2}+cos^2\frac{x}{2}+2.sin\frac{x}{2}.cos\frac{x}{2}$

$=\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2$

$d)$

$1+2cos\left(x\right)$

$=2\left(\frac{1}{2}+cosx\right)$

$=2\left(cos60^o+cosx\right)$

$=4\left(cos\frac{60^o+x}{2}cos\frac{60^o-x}{2}\right)$

$=4cos\left(30^o+\frac{x}{2}\right)cos\left(30^o-\frac{x}{2}\right)$

Đúng(0)

Pham Trong Bach

1 tháng 5 2017

Cho biểu thức P = sin⁡5 x+sin⁡3 x. Biến đổi biểu thức P thành tích ta được kết quả là:

A. P = 2sin⁡4x.cos⁡x

B. P = sin⁡8x

C. P = 8sin⁡x

D. P = 2sin⁡8x.cos⁡2 x

#Toán lớp 10

Cao Minh Tâm

1 tháng 5 2017

Đáp án A

Ta có:

Đề kiểm tra 15 phút Đại số 10 Chương 6 có đáp án (Đề 3)

Đúng(0)

giang quynh anh

4 tháng 5 2021 - olm

biến đổi biểu thức sau thành dạng tích M = sinx-cos2x-sin3x.

#Toán lớp 10

Sách Giáo Khoa

30 tháng 3 2017

Biến đỏi thành tích các biểu thức sau :

a) $1-\sin x$

b) $1+\sin x$

c) $1+2\cos x$

d) $1-2\sin x$

#Toán lớp 10

qwerty

30 tháng 3 2017

a) 1 - sinx = sin $\frac{\prod }{2}$ - sinx = 2cos $\frac{\frac{\prod }{2}+x}{2}$ sin $\frac{\frac{\prod }{2}-x}{2}$

= 2cos $\left ( \frac{\prod }{4} +\frac{x}{2}\right )$ sin $\left ( \frac{\prod }{4} -\frac{x}{2}\right )$

a) 1 + sinx = sin $\frac{\prod }{2}$ + sinx = 2sin $\left ( \frac{\prod }{4} +\frac{x}{2}\right )$ cos $\left ( \frac{\prod }{4} -\frac{x}{2}\right )$

c) 1 + 2cosx = 2( $\frac{1}{2}$ + cosx) = 2(cos $\frac{\prod }{3}$ + cosx) = 4cos $\left ( \frac{\prod }{6} +\frac{x}{2}\right )$ cos $\left ( \frac{\prod }{6} -\frac{x}{2}\right )$

d) 1 - 2sinx = 2( $\frac{1}{2}$ - sinx) = 2(sin $\frac{\prod }{6}$ - sinx) = 4cos $\left ( \frac{\prod }{12} +\frac{x}{2}\right )$ sin $\left ( \frac{\prod }{12} -\frac{x}{2}\right )$

Đúng(0)

Quoc Tran Anh Le

Giáo viên

28 tháng 9 2023

Khai triển các biểu thức sau:

a) ${\left( {4y - 1} \right)^4}$

b) ${\left( {3x + 4y} \right)^5}$

#Toán lớp 10

Hà Quang Minh

Giáo viên

28 tháng 9 2023

a) ${\left( {4y - 1} \right)^4} = {\left[ {4y + \left( { - 1} \right)} \right]^4} = 256{y^4} - 256{y^3} + 96{y^2} - 16y + 1$

b) ${\left( {3x + 4y} \right)^5} = 243{x^5} + 1620{x^4}y + 4320{x^3}{y^2} + 5760{x^2}{y^3} + 3840x{y^4} + 1024{y^5}$

Đúng(0)

Quoc Tran Anh Le

Giáo viên

28 tháng 9 2023

Khai triển các biểu thức sau:

a) ${\left( {x + 1} \right)^5}$

b) ${\left( {x - 3y} \right)^5}$

#Toán lớp 10

Hà Quang Minh

Giáo viên

28 tháng 9 2023

a) ${\left( {x + 1} \right)^5} = {x^5} + 5.{x^4}.1 + 10.{x^3}{.1^2} + 10.{x^2}{.1^3} + 5.{x^1}{.1^4} +{1^5} = {x^5} + 5{x^4} + 10{x^3} + 10{x^2} + 5x + 1$

b) $\begin{array}{l}{\left( {x - 3y} \right)^5} = {\left[ {x + \left( { - 3y} \right)} \right]^5} = {x^5} + 5{x^4}{\left( { - 3y} \right)^1} + 10{x^3}{\left( { - 3y} \right)^2} + 10{x^2}{\left( { - 3y} \right)^3} + 5{x^1}{\left( { - 3y} \right)^4} + {\left( { - 3y} \right)^5}\\ = {x^5} - 15{x^4}y + 90{x^3}{y^2} - 270{x^2}{y^3} + 405x{y^4} - 243{y^5}\end{array}$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP