Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
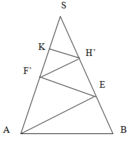
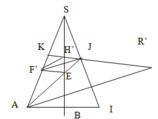
Gọi F’,H’ là điểm đối xứng của F,H qua SO
( O là tâm của đáy)
⇒ EF'=EF, FH=F'H'
Gọi I,J là điểm đối xứng của A,F’ qua SB
⇒
EF
'
=
EJ
,
F
'
H
'
=
H
'
J
A
E
+
EF'+F'H'+H'K=AE+EJ
+
H
'
J
+
H
'
K
≥
AJ
+
K
J
Gọi R là điểm đối xứng của A qua SI ⇒ AJ = J R
⇒
AJ
+
K
J
=
J
R
+
K
J
≥
K
R
Vậy để AE+EF’+F’H’+H’K nhỏ nhất bằng KR thì
H
'
J
+
H
'
K
=
K
J
A
E
+
EJ
=
AJ
=
J
R
k
=
H
F
+
H
K
E
A
+
EF
=
H
'
F
'
+
H
'
K
E
A
+
EF'
=
K
J
J
R
=
S
K
S
A
=
1
2

Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
![]()
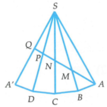
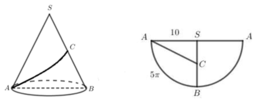
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a

Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2

Đáp án C
Trải khối chóp đều S.ABCD ra mặt phẳng như hình vẽ bên:

Với điểm A=A' và H là trung điểm của AA'
Dễ thấy để A M + M N + N P + P Q nhỏ nhất <=> các điểm A, M, N, P, Q thẳng hàng ⇒ A M + M N + N P + P Q = A Q
Tam giác SAA' có A S A ⏜ = 4 A S B ⏜ = 4 π − 2 11 π 24 = π 3
Mà S A = S A ' ⇒ Δ S A A ' là tam giác đều ⇒ A Q = a 3 2

Đáp án D
Phương pháp:
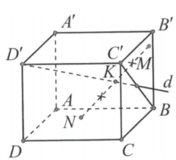
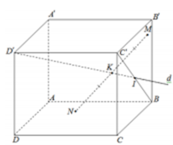
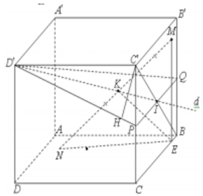
- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)
- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).
Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.
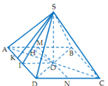
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.
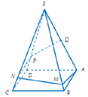

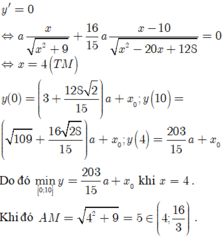





Đáp án A
Phương pháp:
Trải 4 mặt của hình chóp ra mặt phẳng và tìm điều kiện để A M + M N + N P + P Q là nhỏ nhất.
Cách giải:
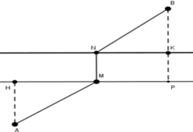
Ta “xếp” 4 mặt của hình chóp lên một mặt phẳng, được như hình bên:
Như hình vẽ ta tháy, để tiết kiệm dây nhất thì các đoạn AM, MN, NP, PQ phải tạo thành một đoạn thẳng AQ.
Lúc này, xét Δ S A Q có:
A S M = M S N = N S P = P S Q = 15 °
S A = 600 m , S Q = 300 m
⇒ k = A M + M N N P + P Q = A N N Q = S A S Q = 2
(Vì A N N Q = S A S Q do tính chất của đường phân giác SN).