Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 8:
$(x-1)(2+x)>0$ thì có 2 TH xảy ra:
TH1: \(\left\{\begin{matrix} x-1>0\\ x+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>1\\ x>-2\end{matrix}\right.\Rightarrow x>1\)
TH2: \(\left\{\begin{matrix} x-1< 0\\ x+2< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< 1\\ x< -2\end{matrix}\right.\Rightarrow x< -2\)
Vậy $x\in (1;+\infty)$ hoặc $x\in (-\infty; -2)$
Câu 7:
$|x^2+x-12|=|(x-3)(x+4)|$
Nếu $x\geq 3$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Nếu $3> x> -4(1)$ thì $(x-3)(x+4)< 0$
$\Rightarrow |x^2+x-12|=-(x^2+x-12)$
BPT trở thành: $-(x^2+x-12)< x^2+x+12$
$\Leftrightarrow 2(x^2+x)>0\Leftrightarrow x>0$ hoặc $x< -1$
Kết hợp với $(1)$ suy ra $3>x>0$ hoặc $-1> x> -4$
Nếu $x\leq -4$ thì $(x-3)(x+4)\geq 0$
$\Rightarrow |x^2+x-12|=x^2+x-12$
BPT trở thành: $x^2+x-12< x^2+x+12$ (luôn đúng)
Vậy BPT có nghiệm $x\in (+\infty; 0)$ hoặc $x\in (-\infty; -1)$

a) Gọi D là điều kiện xác định của biểu thức vế trái D = [- 8; +∞]. Vế trái dương với mọi x ∈ D trong khi vế phải là số âm. Mệnh đề sai với mọi x ∈ D. Vậy bất phương trình vô nghiệm.
b) Vế trái có ≥ 1 ∀x ∈ R,
≥ 1 ∀x ∈ R
=> +
≥ 2 ∀x ∈ R.
Mệnh đề sai ∀x ∈ R. Bất phương trình vô nghiệm.
c) ĐKXĐ: D = [- 1; 1]. Vế trái âm với mọi x ∈ D trong khi vế phải dương.

1.
\(\left\{{}\begin{matrix}x>2\\\frac{5}{2}+3\le x+\frac{3}{2}x\\2x\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>2\\\frac{5}{2}x\ge\frac{11}{2}\\x\le\frac{5}{2}\end{matrix}\right.\) \(\Rightarrow\frac{11}{5}\le x\le\frac{5}{2}\)
\(\Rightarrow a+b=\frac{11}{5}+\frac{5}{2}=D\)
2.
\(\left\{{}\begin{matrix}6x-4x>7-\frac{5}{7}\\4x-2x< 25-\frac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>\frac{22}{7}\\x< \frac{47}{4}\end{matrix}\right.\)
\(\Rightarrow\frac{22}{7}< x< \frac{47}{4}\Rightarrow x=\left\{4;5...;11\right\}\) có 8 giá trị
3.
\(\left\{{}\begin{matrix}5x-4x< 5+2\\x^2< x^2+4x+4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< 7\\x>-1\end{matrix}\right.\)
\(\Rightarrow-1< x< 7\Rightarrow x=\left\{0;1;...;6\right\}\)
\(\Rightarrow\sum x=1+2+...+6=21\)
4.
\(\left\{{}\begin{matrix}x^2-2x+1\le8-4x+x^2\\x^3+6x^2+12x+8< x^3+6x^2+13x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\le7\\x\ge-1\end{matrix}\right.\) \(\Rightarrow-1\le x\le\frac{7}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{min}=-1\\x_{max}=3\end{matrix}\right.\) \(\Rightarrow S=2\)
5.
\(\left\{{}\begin{matrix}x>\frac{1}{2}\\x< m+2\end{matrix}\right.\)
Hệ đã cho có nghiệm khi và chỉ khi:
\(m+2>\frac{1}{2}\Rightarrow m>-\frac{3}{2}\)

lời giải
a)
\(\left(x+1\right)\left(2x-1\right)+x\le2x^2+3\)
\(\Leftrightarrow2x^2+x-1+x\le2x^2+3\)
\(\Leftrightarrow2x\le4\Rightarrow x\le2\)
\(\)b) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)-x>x^3+6x^2-5\)
\(\left(x^2+3x+2\right)\left(x+3\right)-x>x^3+6x^2-5\)
\(x^3+3x^2+3x^2+9x+2x+6-x>x^3+6x^2-5\)
\(10x+6>-5\Rightarrow x>-\dfrac{11}{10}\)
c)Đkxđ: x≥0
x+√x>(2√x+3)(√x−1)
⇔x+√x>2x+√x−3
⇔x−3>0
⇔x>3. (tmđk).
Chọn D.
Điều kiện: x < 3
Vì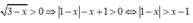
Vậy tập nghiệm của bất phương trình là S = (- ∞ ;1)